11. 如图是一个算法的流程图,则输出K值是( )
如图是一个算法的流程图,则输出K值是( )
 如图是一个算法的流程图,则输出K值是( )
如图是一个算法的流程图,则输出K值是( )| A. | 6 | B. | 7 | C. | 16 | D. | 19 |
10.17世纪日本数学家们对这个数学关于体积方法的问题还不了解,他们将体积公式“V=kD3”中的常数k称为“立圆术”或“玉积率”,创用了求“玉积率”的独特方法“会玉术”,其中,D为直径,类似地,对于等边圆柱(轴截面是正方形的圆柱叫做等边圆柱)、正方体也有类似的体积公式V=kD3,其中,在等边圆柱中,D表示底面圆的直径;在正方体中,D表示棱长,假设运用此“会玉术”,求得的球、等边圆柱、正方体的“玉积率”分别为k1,k2,k3=( )
| A. | $\frac{π}{4}$:$\frac{π}{6}$:1 | B. | $\frac{π}{6}$:$\frac{π}{4}$:2 | C. | 1:3:$\frac{12}{π}$ | D. | 1:$\frac{3}{2}$:$\frac{6}{π}$ |
9.将一条均匀木棍随机折成两段,则其中一段大于另一段三倍的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
8.已知变量x,y满足约束条件$\left\{\begin{array}{l}{y≤2}\\{x+y≥1}\\{x-y≤1}\end{array}\right.$,则z=3x+y的最小值为( )
| A. | -1 | B. | 1 | C. | 0 | D. | 11 |
7.已知等比数列{an}中,a3a9=2a52,且a3=2,则a5=( )
| A. | -4 | B. | 4 | C. | -2 | D. | 2 |
6.已知向量$\overrightarrow{a}$=(-1,2),b=(0,3),如果向量$\overrightarrow{a}$+2$\overrightarrow{b}$与$\overrightarrow{a}$-x$\overrightarrow{b}$垂直,则实数x的值为( )
0 239105 239113 239119 239123 239129 239131 239135 239141 239143 239149 239155 239159 239161 239165 239171 239173 239179 239183 239185 239189 239191 239195 239197 239199 239200 239201 239203 239204 239205 239207 239209 239213 239215 239219 239221 239225 239231 239233 239239 239243 239245 239249 239255 239261 239263 239269 239273 239275 239281 239285 239291 239299 266669
| A. | 1 | B. | -1 | C. | $\frac{17}{24}$ | D. | -$\frac{17}{24}$ |
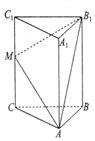 如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,AC=BC=5,AB=6,M是CC1中点,CC1=8.
如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,AC=BC=5,AB=6,M是CC1中点,CC1=8.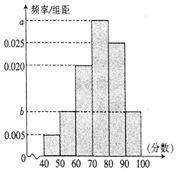 某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图,其中前三段的频率成等比数列.
某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图,其中前三段的频率成等比数列.