题目内容

7．已知等比数列{an}中，a3a9=2a52，且a3=2，则a5=（　　）
A．-4B．4C．-2D．2

分析 由等比数列项公式推导出${{a}_{5}}^{2}={a}_{1}{a}_{9}$，从而a1=1，由等比中项的性质得${a}_{1}{a}_{5}={{a}_{3}}^{2}$，由此能求出a5．

解答 解：∵等比数列{an}中，a3a9=2a52，且a3=2，
∴$2{a}_{9}=2{{a}_{5}}^{2}$．
∵${{a}_{5}}^{2}={a}_{1}{a}_{9}$，∴a1=1，
由等比中项的性质得${a}_{1}{a}_{5}={{a}_{3}}^{2}$，
∴a5=$\frac{{{a}_{3}}^{2}}{{a}_{1}}$=4．
故选：B．

点评 本题考查等比数列的第5项的求法，考查等比数列的通项公式、前n项和公式等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想，函数与方程思想，是基础题．

练习册系列答案
相关题目
17．对于无穷数列{an}，记T={x|x=aj-ai，i＜j}，若数列{an}满足：“存在t∈T，使得只要am-ak=t（m，k∈N*且m＞k），必有am+1-ak+1=t”，则称数列{an}具有性质P（t）．
（Ⅰ）若数列{an}满足${a_n}=\left\{{\begin{array}{l}{2n，n≤2}\\{2n-5，n≥3}\end{array}}\right.$判断数列{an}是否具有性质P（2）？是否具有性质P（4）？
（Ⅱ）求证：“T是有限集”是“数列{an}具有性质P（0）”的必要不充分条件；
（Ⅲ）已知{an}是各项为正整数的数列，且{an}既具有性质P（2），又具有性质P（5），求证：存在整数N，使得aN，aN+1，aN+2，…，aN+k，…是等差数列．
18．已知复数z满足i•z=3-4i（其中i为虚数单位），则|z|=5．
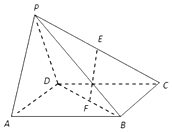15．底面是正方形的四棱锥中P-ABCD中，侧面PAD⊥底面ABCD，且△PAD是等腰直角三角形，其中PA=PD，E，F分别为线段PC，DB的中点，问在线段AB上是否存在点G，使得二面角C-PD-G的余弦值为$\frac{{\sqrt{3}}}{3}$，若存在，请求出点G的位置；若不存在，请说明理由．
2．“更相减损术”是出自《九章算术》的一种求最大公约数的算法，如框图中若输入的a、b分别为198、90，则输出的i为（　　）
A．3B．4C．5D．6
12．直线y=4x与曲线y=x2围成的封闭区域面积为$\frac{32}{3}$．
19．若复数z=$\frac{3-i}{i}$的共轭复数为$\overline{z}$，则$\overline{z}$在复平面内的对应点位于（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
16．在△ABC中，角A，B，C所对的边分别为a，b，c，且B=60°，c=4．
（Ⅰ）若b=6，求角C的正弦值及△ABC的面积；
（Ⅱ）若D，E在线段BC上，且BD=DE=EC，$AE=2\sqrt{3}BD$，求AD的长．
16．已知向量$\overrightarrow{a}$=（2sinx-1，sin（2x+$\frac{π}{3}$）），$\overrightarrow{b}$=（1，cos（2x+$\frac{π}{6}$）），$\overrightarrow{c}$=（cosx，1），f（x）=（$\overrightarrow{a}$+$\overrightarrow{b}$）•$\overrightarrow{c}$
（1）求函数f（x）在[0，π]上的单调递增区间；
（2）△ABC的角A，B，C的对边长分别为a，b，c，且a2，b2，c2成等差数列，求f（B）的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网