15.已知A,B为抛物线E:y2=2px(p>0)上异于顶点O的两点,△AOB是等边三角形,其面积为48$\sqrt{3}$,则p的值为( )
| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{3}$ |
14. 执行如图所示的程序框图,若输出的S的值为12,则输入的a值可以为( )
执行如图所示的程序框图,若输出的S的值为12,则输入的a值可以为( )
 执行如图所示的程序框图,若输出的S的值为12,则输入的a值可以为( )
执行如图所示的程序框图,若输出的S的值为12,则输入的a值可以为( )| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
13.已知实数x,y满足约束条件$\left\{\begin{array}{l}{x≥2}\\{x+y≥4}\\{2x-y-12≤0}\end{array}\right.$,则目标函数z=3x+y的最小值为( )
| A. | -8 | B. | -2 | C. | 8 | D. | $\frac{44}{3}$ |
12.复数z满足(1+$\sqrt{3}$i)z=4,则|z|等于( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
11.已知全集为R,集合A={x|x2-2x<3},B={x|x>2},则A∩(∁RB)( )
| A. | {x|-1<x<2} | B. | {x|2<x<3} | C. | {x|x<3} | D. | {x|-1<x≤2} |
6.市政府为调查市民对本市某项调控措施的态度,随机抽取了100名市民,统计了他们的月收入频率分布和对该项措施的赞成人数,统计结果如表所示:
(1)用样本估计总体的思想比较该市月收入低于20(百元)和不低于30(百元)的类人群在该项措施的态度上有何不同;
(2)现从上班中月收入在[10,20)和[60,70)的市民中各随机抽取一个进行跟踪调查,求抽取的两个人恰好对该措施一个赞成一个不赞成的概率.
0 239013 239021 239027 239031 239037 239039 239043 239049 239051 239057 239063 239067 239069 239073 239079 239081 239087 239091 239093 239097 239099 239103 239105 239107 239108 239109 239111 239112 239113 239115 239117 239121 239123 239127 239129 239133 239139 239141 239147 239151 239153 239157 239163 239169 239171 239177 239181 239183 239189 239193 239199 239207 266669
| 月收入(单位:百元) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70) |
| 频数 | 5 | 20 | 30 | 31 | 10 | 4 |
| 赞成人数 | 2 | 14 | 24 | 30 | 7 | 3 |
(2)现从上班中月收入在[10,20)和[60,70)的市民中各随机抽取一个进行跟踪调查,求抽取的两个人恰好对该措施一个赞成一个不赞成的概率.
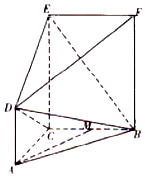 在如图所示的五面体ABCDEF中,矩形BCEF所在的平面ABC垂直,AD∥CE,CE=2AD=2,M是BC的中点,在△ABC中,∠BAC=60°,AB=2AC=2.
在如图所示的五面体ABCDEF中,矩形BCEF所在的平面ABC垂直,AD∥CE,CE=2AD=2,M是BC的中点,在△ABC中,∠BAC=60°,AB=2AC=2.