题目内容
14. 执行如图所示的程序框图,若输出的S的值为12,则输入的a值可以为( )
执行如图所示的程序框图,若输出的S的值为12,则输入的a值可以为( )| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
分析 模拟程序的运行,依次写出每次循环得到的S,i的值,由题意可得当输出的S的值为12时,可得7≤a<10,即可得解.
解答 解:模拟程序的运行,可得
S=0,i=1
执行循环体,S=1,i=4
不满足条件i>a,执行循环体,S=5,i=7
不满足条件i>a,执行循环体,S=12,i=10
由题意,此时应该满足条件10>a,退出循环,输出S的值为12.
故7≤a<10.
故选:A.
点评 本题主要考查了循环结构的程序框图的应用,由退出循环的条件得到a的取值范围是解题的关键,属于基础题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
5.下列命题中,错误的是( )
| A. | ?x∈(0,$\frac{π}{2}$),x>sinx | |
| B. | 在△ABC中,若A>B,则sinA>sinB | |
| C. | 函数f(x)=tanx图象的一个对称中心是($\frac{π}{2}$,0) | |
| D. | ?x0∈R,sinx0cosx0=$\frac{\sqrt{2}}{2}$ |
2.设复数z与$\frac{1+3i}{1-i}$在复平面内对应的点关于实轴对称,则z等于( )
| A. | -1+2i | B. | 1+2i | C. | 1-2i | D. | -1-2i |
6.已知抛物线C:y2=4x,过焦点F且斜率为$\sqrt{3}$的直线与C相交于P,Q两点,且P,Q两点在准线上的投影分别为M,N两点,则S△MFN=( )
| A. | $\frac{8}{3}$ | B. | $\frac{{8\sqrt{3}}}{3}$ | C. | $\frac{16}{3}$ | D. | $\frac{{16\sqrt{3}}}{3}$ |
3.执行如图的程序框图,则输出的S=( )

| A. | 2 | B. | -3 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{3}$ |
4.已知P={x|x2+2x-3<0},Q={-2,-1,0,1,2},则P∩Q=( )
| A. | {-1,0,1} | B. | {-2,-1,0,1} | C. | {-2,-1,0} | D. | {-1,0} |
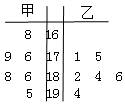 在一次水稻试验田验收活动中,将甲、乙两种水稻随机抽取各6株样品,单株籽粒数制成如图所示的茎叶图:
在一次水稻试验田验收活动中,将甲、乙两种水稻随机抽取各6株样品,单株籽粒数制成如图所示的茎叶图: