15.设函数$f(x)=({{x^2}-2x})lnx+({a-\frac{1}{2}}){x^2}+2({1-a})x+a$.
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)当a<-2时,讨论f(x)的零点个数.
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)当a<-2时,讨论f(x)的零点个数.
14.对某地区儿童的身高与体重的一组数据,我们用两种模型①y=bx+a,②y=cedx拟合,得到回归方程分别为${\widehaty^{(1)}}=0.24x-8.81$,${\widehaty^{(2)}}=1.70{e^{0.022x}}$,作残差分析,如表:
(Ⅰ)求表中空格内的值;
(Ⅱ)根据残差比较模型①,②的拟合效果,决定选择哪个模型;
(Ⅲ)残差大于1kg的样本点被认为是异常数据,应剔除,剔除后对(Ⅱ)所选择的模型重新建立回归方程.
(结果保留到小数点后两位)
附:对于一组数据(x1,y1),(x2,y2),…(xn,yn),其回归直线y=bx+a的斜率和截距的最小二乘法估计分别为$\widehatb=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.
0 238987 238995 239001 239005 239011 239013 239017 239023 239025 239031 239037 239041 239043 239047 239053 239055 239061 239065 239067 239071 239073 239077 239079 239081 239082 239083 239085 239086 239087 239089 239091 239095 239097 239101 239103 239107 239113 239115 239121 239125 239127 239131 239137 239143 239145 239151 239155 239157 239163 239167 239173 239181 266669
| 身高x(cm) | 60 | 70 | 80 | 90 | 100 | 110 |
| 体重y(kg) | 6 | 8 | 10 | 14 | 15 | 18 |
| ${\widehate^{(1)}}$ | 0.41 | 0.01 | 1.21 | -0.19 | 0.41 | |
| ${\widehate^{(2)}}$ | -0.36 | 0.07 | 0.12 | 1.69 | -0.34 | -1.12 |
(Ⅱ)根据残差比较模型①,②的拟合效果,决定选择哪个模型;
(Ⅲ)残差大于1kg的样本点被认为是异常数据,应剔除,剔除后对(Ⅱ)所选择的模型重新建立回归方程.
(结果保留到小数点后两位)
附:对于一组数据(x1,y1),(x2,y2),…(xn,yn),其回归直线y=bx+a的斜率和截距的最小二乘法估计分别为$\widehatb=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.
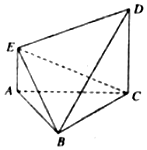 如图,△ABC为边长为2的正三角形,AE∥CD,且AE⊥平面ABC,2AE=CD=2.
如图,△ABC为边长为2的正三角形,AE∥CD,且AE⊥平面ABC,2AE=CD=2.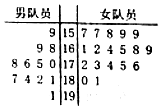 为了检验训练情况,武警某支队于近期举办了一场展示活动,其中男队员12人,女队员18人,测试结果如茎叶图所示(单位:分).若成绩不低于175分者授予“优秀警员”称号,其他队员则给予“优秀陪练员”称号.
为了检验训练情况,武警某支队于近期举办了一场展示活动,其中男队员12人,女队员18人,测试结果如茎叶图所示(单位:分).若成绩不低于175分者授予“优秀警员”称号,其他队员则给予“优秀陪练员”称号.