18.曲线y=eaxcosx在x=0处的切线与直线x+2y=0垂直,则a=( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
17.类比平面内三角形“三边垂直平分线的交点是三角形外接圆圆心”的性质,可推知四面体的下列性质( )
| A. | 过四面体各面的垂心分别与各面垂直的直线交点为四面体外接球球心 | |
| B. | 过四面体各面的内心分别与各面垂直的直线交点为四面体外接球球心 | |
| C. | 过四面体各面的重心分别与各面垂直的直线交点为四面体外接球球心 | |
| D. | 过四面体各面的外心分别与各面垂直的直线交点为四面体外接球球心 |
16.已知i是虚数单位,$\overline z$是复数z的共轭复数,$\overline z+|z|•i=1+2i$,则z的虚部为( )
| A. | $-\frac{3}{4}$ | B. | $\frac{3}{4}$ | C. | $-\frac{3}{4}i$ | D. | $\frac{3}{4}i$ |
15.设a、b∈(0,+∞),则“ab<ba”是“a>b>e”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
14.已知四棱锥P-ABCD中,$\overrightarrow{AB}=({4,-2,3})$,$\overrightarrow{AD}=({-4,1,0})$,$\overrightarrow{AP}=({-6,2,-8})$,则点P到底面ABCD的距离为( )
| A. | $\frac{{\sqrt{26}}}{13}$ | B. | $\frac{{\sqrt{26}}}{26}$ | C. | 1 | D. | 2 |
13.已知x,y是实数,i是虚数单位,$\frac{x}{1+i}=1-yi$,则复数x+yi在复平面内对应的点位于( )
0 238933 238941 238947 238951 238957 238959 238963 238969 238971 238977 238983 238987 238989 238993 238999 239001 239007 239011 239013 239017 239019 239023 239025 239027 239028 239029 239031 239032 239033 239035 239037 239041 239043 239047 239049 239053 239059 239061 239067 239071 239073 239077 239083 239089 239091 239097 239101 239103 239109 239113 239119 239127 266669
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
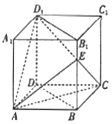 如图,在各棱长均为4的直四棱柱ACCD-A1B1C1D1中,底面ABCD为菱形,∠BAD=60°,E为梭BB1上一点,且BE=3EB1
如图,在各棱长均为4的直四棱柱ACCD-A1B1C1D1中,底面ABCD为菱形,∠BAD=60°,E为梭BB1上一点,且BE=3EB1