6.已知f(x)=$\left\{\begin{array}{l}{ln(1-x),x<0}\\{{x}^{2}-ax,x≥0}\end{array}\right.$,且g(x)=f(x)+$\frac{x}{2}$有三个零点,则实数a的取值范围为( )
| A. | ($\frac{1}{2}$,+∞) | B. | [1,+∞) | C. | (0,$\frac{1}{2}$ ) | D. | (0,1] |
4.已知f(x)=2x2-4x-1,设有n个不同的数xi(i=1,2,…,n)满足0≤x1<x2<…<xn≤3,则满足|f(x1)-f(x2)|+|f(x2)-f(x3)|+…+|f(xn-1)-f(xn)|≤M的M的最小值是( )
| A. | 10 | B. | 8 | C. | 6 | D. | 2 |
3.设x、y满足不等式组$\left\{\begin{array}{l}{x-2y+1≤0}\\{2x+y-6≤0}\\{x-y+a≥0}\end{array}\right.$,其中a为常数,当且仅当x=y=1时,目标函数z=x+2y取得最小值,则目标函数z的最大值为( )
| A. | 8 | B. | $\frac{27}{5}$ | C. | 6 | D. | 3 |
1.设函数f(x)与函数g(x)是定义在同一区间上的两个函数,若函数y=f(x)-g(x)在次区间上有两个不同的零点,则称函数f(x),g(x)在此区间上是“交织函数”,若f(x)=4|x|-$\frac{9}{4}$与g(x)=2x+m在(-∞,+∞)上是“交织函数”,则m的取值范围为( )
| A. | (-$\frac{9}{4}$,-2] | B. | [-1,0] | C. | (-∞,-2] | D. | (-$\frac{9}{4}$,+∞) |
12.为了得到函数$y=3sin(2x+\frac{π}{5})$的图象,只需把y=3sin2x上的所有的点( )
| A. | 向左平行移动$\frac{π}{10}$长度单位 | B. | 向右平行移动$\frac{π}{10}$长度单位 | ||
| C. | 向右平行移动$\frac{π}{5}$长度单位 | D. | 向左平行移动$\frac{π}{5}$长度单位 |
11.已知经过点P(3,m)和点Q(m,-2)的直线的斜率等于2,则m的值为( )
| A. | $\frac{4}{3}$ | B. | 1 | C. | 2 | D. | -1 |
10.cos135°的值为( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $-\frac{{\sqrt{2}}}{2}$ |
9.函数f(x)=e2x+2cosx-4在[0,2π]上是( )
0 238852 238860 238866 238870 238876 238878 238882 238888 238890 238896 238902 238906 238908 238912 238918 238920 238926 238930 238932 238936 238938 238942 238944 238946 238947 238948 238950 238951 238952 238954 238956 238960 238962 238966 238968 238972 238978 238980 238986 238990 238992 238996 239002 239008 239010 239016 239020 239022 239028 239032 239038 239046 266669
| A. | 在[0,π]上是减函数,[0,2π]上是增函数 | B. | [0,π]在上是增函数,[0,2π]上是减函数 | ||
| C. | 增函数 | D. | 减函数 |
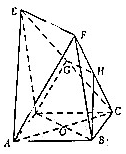 如图,在多面体ABCDEF中,底面ABCD是边长为1的正方形,四边形BDEF是矩形,且BF=2,CF=$\sqrt{5}$,G和H分别是CE和CF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为1的正方形,四边形BDEF是矩形,且BF=2,CF=$\sqrt{5}$,G和H分别是CE和CF的中点.