题目内容
3．设x、y满足不等式组$\left\{\begin{array}{l}{x-2y+1≤0}\\{2x+y-6≤0}\\{x-y+a≥0}\end{array}\right.$，其中a为常数，当且仅当x=y=1时，目标函数z=x+2y取得最小值，则目标函数z的最大值为（ ）| A． | 8 | B． | $\frac{27}{5}$ | C． | 6 | D． | 3 |
分析 由题意可得y=x+a过点（1，1），求得a，作出其平面区域，进而找到目标函数z有最大值时的点C，解出点C代入即可．
解答 
解：由题意可得y=x+a过点（1，1），
故a=0．
作出其平面区域如右图：
则由图象知，
平移直线x+2y=0，可得目标函数z=x+2y过点C时，有最大值．
由$\left\{\begin{array}{l}{x-y=0}\\{2x+y-6=0}\end{array}\right.$，易知C（2，2）
则目标函数z=x+2y的最大值为2+2×2=6．
故选：C．
点评 本题考查了线性规划的应用，注意运用平移法，以及数形结合法，考查运算能力，属于中档题．
练习册系列答案
相关题目
6．执行如图所示的程序框图，则输出的结果是（ ）
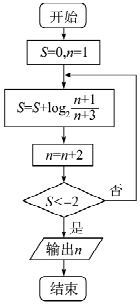
| A． | 7 | B． | 8 | C． | 9 | D． | 10 |
10．cos135°的值为（ ）
| A． | $\frac{1}{2}$ | B． | $-\frac{1}{2}$ | C． | $\frac{{\sqrt{2}}}{2}$ | D． | $-\frac{{\sqrt{2}}}{2}$ |
8．已知函数 f（x）=x+$\frac{2b}{x}$+a，x∈[a，+∞），其中a＞0，b∈R，记m（a，b）为 f（x）的最小值，则当m（a，b）=2时，b的取值范围为（ ）
| A． | b＞$\frac{1}{3}$ | B． | b＜$\frac{1}{3}$ | C． | b＞$\frac{1}{2}$ | D． | b＜$\frac{1}{2}$ |