题目内容
6.已知f(x)=$\left\{\begin{array}{l}{ln(1-x),x<0}\\{{x}^{2}-ax,x≥0}\end{array}\right.$,且g(x)=f(x)+$\frac{x}{2}$有三个零点,则实数a的取值范围为( )| A. | ($\frac{1}{2}$,+∞) | B. | [1,+∞) | C. | (0,$\frac{1}{2}$ ) | D. | (0,1] |
分析 根据图象得出g(x)在(-∞,0)上的零点个数,得出g(x)在[0,+∞)上的零点个数,利用二次函数的性质得出a的范围.
解答 解:令g(x)=0得f(x)=-$\frac{x}{2}$,
作出f(x)=ln(1-x)与y=-$\frac{x}{2}$的函数图象,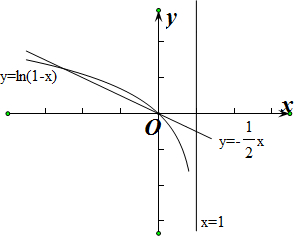
由图象可知f(x)与y=-$\frac{x}{2}$在(-∞,0)上只有1个交点,
∴g(x)=0在(-∞,0)上只有1个零点,
∴f(x)=-$\frac{1}{2}x$在[0,+∞)上有2个零点,即得到x2-ax+$\frac{x}{2}$=0在[0,+∞)上有两解,
解方程x2-ax+$\frac{x}{2}$=0得x1=0,x2=a-$\frac{1}{2}$,
∴a-$\frac{1}{2}$>0,即a$>\frac{1}{2}$.
故选A.
点评 本题考查了函数零点与函数图象的关系,属于中档题.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
8.在数列{an}中,若$\sqrt{{a}_{n+1}}$=$\sqrt{{a}_{n}}$+$\sqrt{2}$,a1=8,则数列{an}的通项公式为( )
| A. | an=2(n+1)2 | B. | an=4(n+1) | C. | an=8n2 | D. | an=4n(n+1) |
9.欧拉公式eix=cosx+isinx (i为虚数单位)是瑞士数学家欧拉发明的,将指数的定义域扩大到复数集,建立了三角函数和指数函数的联系,被誉为“数学中的天桥”.根据欧拉公式可知,e${\;}^{\frac{π}{3}i}$表示的复数的模为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{π}{3}$ |
6.某小卖部为了了解热茶销售量y(杯)与气温x(℃)之间的关系,随机统计了某4天卖出的热茶的杯数与当天气温,并制作了对照表:
由表中数据算得线性回归方程$\stackrel{∧}{y}$=bx+a中的b=-2,预测当气温为-5°时,热茶销售量为( )
| 气温(℃) | 18 | 13 | 10 | -1 |
| 杯数 | 24 | 34 | 38 | 64 |
| A. | 70 | B. | 50 | C. | 60 | D. | 80 |
1.设函数f(x)与函数g(x)是定义在同一区间上的两个函数,若函数y=f(x)-g(x)在次区间上有两个不同的零点,则称函数f(x),g(x)在此区间上是“交织函数”,若f(x)=4|x|-$\frac{9}{4}$与g(x)=2x+m在(-∞,+∞)上是“交织函数”,则m的取值范围为( )
| A. | (-$\frac{9}{4}$,-2] | B. | [-1,0] | C. | (-∞,-2] | D. | (-$\frac{9}{4}$,+∞) |
18.已知命题p:?x0∈R,2x0+1≤0,则命题p的否定是( )
| A. | ?x0∈R,2x0+1>0 | B. | ?x∈R,2x+1>0 | C. | ?x0∈R,2x0+1≤0 | D. | ?x∈R,2x+1≥0 |
16.复数z=3i(i+1)的实部与虚部分别为( )
| A. | 3,3 | B. | -3,-3i | C. | -3,3 | D. | -3,3i |