18．一元二次方程x2-2ix-5=0的根的情况是（ ）
| A． | 有两个不等的实根 | B． | 有一个实根和一个虚根 | ||
| C． | 有一对共轭的虚根 | D． | 有两个不共轭的虚根 |
14．
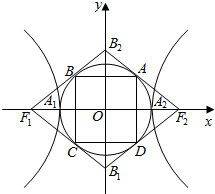我们把离心率为$\frac{\sqrt{5}+1}{2}$的双曲线叫做黄金双曲线．如图，黄金双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a，b＞0）的两顶点为A1，A2，虚轴两端点为B1，B2，两焦点为F1，F2，若以A1，A2为直径的圆内切于菱形F1B1F2B2，切点分别为A，B，C，D，则菱形F1B1F2B2的面积S1与矩形ABCD的面积S2的比值$\frac{{S}_{1}}{{S}_{2}}$=（ ）
我们把离心率为$\frac{\sqrt{5}+1}{2}$的双曲线叫做黄金双曲线．如图，黄金双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a，b＞0）的两顶点为A1，A2，虚轴两端点为B1，B2，两焦点为F1，F2，若以A1，A2为直径的圆内切于菱形F1B1F2B2，切点分别为A，B，C，D，则菱形F1B1F2B2的面积S1与矩形ABCD的面积S2的比值$\frac{{S}_{1}}{{S}_{2}}$=（ ）| A． | $\frac{\sqrt{5}+2}{2}$ | B． | $\frac{\sqrt{5}+1}{2}$ | C． | $\frac{\sqrt{5}-2}{2}$ | D． | $\frac{\sqrt{5}-1}{2}$ |
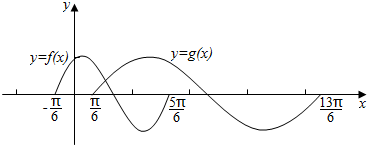
11．如图，是函数y=f（x）=sin（ω1x+φ1）和y=g（x）=sin（ω2x+φ2）在一个周期上的图象，为了得到y=f（x）的图象，只要将y=g（x）的图象上所有的点（ ）
0 225096 225104 225110 225114 225120 225122 225126 225132 225134 225140 225146 225150 225152 225156 225162 225164 225170 225174 225176 225180 225182 225186 225188 225190 225191 225192 225194 225195 225196 225198 225200 225204 225206 225210 225212 225216 225222 225224 225230 225234 225236 225240 225246 225252 225254 225260 225264 225266 225272 225276 225282 225290 266669
| A． | 向左平移$\frac{π}{3}$个单位长度．再把所得点的横坐标伸长到原来的2倍．纵坐标不变 | |
| B． | 向左平移$\frac{π}{3}$个单位长度．再把所得点的横坐标缩短到原来的$\frac{1}{2}$倍．纵坐标不变 | |
| C． | 向左平移$\frac{π}{2}$个单位长度．再把所得点的横坐标伸长到原来的2倍．纵坐标不变 | |
| D． | 向左平移$\frac{π}{2}$个单位长度．再把所得点的横坐标缩短到原来的$\frac{1}{2}$倍．纵坐标不变 |