题目内容
13.已知集合A={x||x-1≤1},B={x|y=$\sqrt{1-3x}$},则A∩B=[0,$\frac{1}{3}$],(∁RA)∪B=(-∞,$\frac{1}{3}$]∪(2,+∞).分析 化简集合A,B,即可得出结论.
解答 解:集合A={x||x-1|≤1}=[0,2],B={x|y=$\sqrt{1-3x}$}=(-∞,$\frac{1}{3}$],
∴A∩B=[0,$\frac{1}{3}$],(∁RA)∪B=(-∞,$\frac{1}{3}$]∪(2,+∞),
故答案为:[0,$\frac{1}{3}$],(-∞,$\frac{1}{3}$]∪(2,+∞).
点评 本题考查集合的运算,考查学生的计算能力,正确化简是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.一元二次方程x2-2ix-5=0的根的情况是( )
| A. | 有两个不等的实根 | B. | 有一个实根和一个虚根 | ||
| C. | 有一对共轭的虚根 | D. | 有两个不共轭的虚根 |
12.(1)若不等式$sin(2x+\frac{π}{3})-\frac{1}{a}>0$对$x∈[\frac{π}{6},\frac{π}{2}]$的所有实数x都成立,求a的取值范围;
(2)若不等式x2-2ax+2a+1>0对0≤x≤1的所有实数x都成立,求a的取值范围;
(3)设a>0且a≠1,f(x)=x2-ax,对x∈(-1,1),均有$f(x)<\frac{1}{2}$,求a的范围.
(4)完成填空
(2)若不等式x2-2ax+2a+1>0对0≤x≤1的所有实数x都成立,求a的取值范围;
(3)设a>0且a≠1,f(x)=x2-ax,对x∈(-1,1),均有$f(x)<\frac{1}{2}$,求a的范围.
(4)完成填空
| 用图象语言表述 | 用函数最值表述 | |
| 在(a,b)内,若对任意的x有f(x)>g(x)成立 | ① | ② |
| 在(a,b)内,若存在x0,使f(x)>g(x)成立 | ③ | ④ |
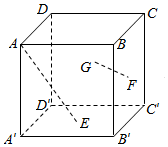 在正方体ABCD-A′B′C′D′中,E,F,G分别是面A′C′,面B′C,面CD′的中心,则AE与FG所成的角大小为多少?
在正方体ABCD-A′B′C′D′中,E,F,G分别是面A′C′,面B′C,面CD′的中心,则AE与FG所成的角大小为多少?