题目内容
18．一元二次方程x2-2ix-5=0的根的情况是（ ）| A． | 有两个不等的实根 | B． | 有一个实根和一个虚根 | ||
| C． | 有一对共轭的虚根 | D． | 有两个不共轭的虚根 |
分析 利用求根公式求出一元二次方程x2-2ix-5=0的两个根，即可得出正确的结论．
解答 解：一元二次方程x2-2ix-5=0中，设两根分别为x1、x2，
因为△=（-2i）2-4×（-5）=16，
解得x1=-2+i，x2=2+i；
所以该一元二次方程有两个不共轭的虚根．
故选：C．
点评 本题考查了利用求根公式解复数系数的一元二次方程的应用问题，是基础题目．
练习册系列答案
小博士期末闯关100分系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
10．设M={$\overrightarrow{a}$|$\overrightarrow{a}$=（2，0）+m（0，1），m∈R}和N={$\overrightarrow{b}$|$\overrightarrow{b}$（1，1）+n=（1，-1），n∈R}都是元素为向量的集合，则M∩N等于（ ）
| A． | {（1，0）} | B． | {（-1，1）} | C． | {（2，0）} | D． | {（2，1）} |
18．
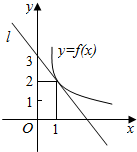如图所示，y=f（x）是可导函数，直线l：y=kx+3是曲线y=f（x）在x=1处的切线，令h（x）=xf（x），h′（x）是h（x）的导函数，则h′（1）的值是（ ）
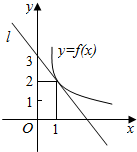如图所示，y=f（x）是可导函数，直线l：y=kx+3是曲线y=f（x）在x=1处的切线，令h（x）=xf（x），h′（x）是h（x）的导函数，则h′（1）的值是（ ）| A． | 2 | B． | 1 | C． | -1 | D． | $\frac{1}{2}$ |