题目内容
14.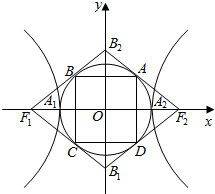 我们把离心率为$\frac{\sqrt{5}+1}{2}$的双曲线叫做黄金双曲线.如图,黄金双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的两顶点为A1,A2,虚轴两端点为B1,B2,两焦点为F1,F2,若以A1,A2为直径的圆内切于菱形F1B1F2B2,切点分别为A,B,C,D,则菱形F1B1F2B2的面积S1与矩形ABCD的面积S2的比值$\frac{{S}_{1}}{{S}_{2}}$=( )
我们把离心率为$\frac{\sqrt{5}+1}{2}$的双曲线叫做黄金双曲线.如图,黄金双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的两顶点为A1,A2,虚轴两端点为B1,B2,两焦点为F1,F2,若以A1,A2为直径的圆内切于菱形F1B1F2B2,切点分别为A,B,C,D,则菱形F1B1F2B2的面积S1与矩形ABCD的面积S2的比值$\frac{{S}_{1}}{{S}_{2}}$=( )| A. | $\frac{\sqrt{5}+2}{2}$ | B. | $\frac{\sqrt{5}+1}{2}$ | C. | $\frac{\sqrt{5}-2}{2}$ | D. | $\frac{\sqrt{5}-1}{2}$ |
分析 菱形F1B1F2B2的面积S1=2bc,求出矩形ABCD的长与宽,从而求出面积S2=4mn=$\frac{4{a}^{2}bc}{{b}^{2}+{c}^{2}}$,由此可得结论.
解答 解:菱形F1B1F2B2的面积S1=2bc
设矩形ABCD,BC=2n,BA=2m,∴$\frac{m}{n}$=$\frac{c}{b}$
∵m2+n2=a2,∴m=$\frac{ac}{\sqrt{{b}^{2}+{c}^{2}}}$,n=$\frac{ab}{\sqrt{{b}^{2}+{c}^{2}}}$
∴面积S2=4mn=$\frac{4{a}^{2}bc}{{b}^{2}+{c}^{2}}$.
∴$\frac{{S}_{1}}{{S}_{2}}$=$\frac{{b}^{2}+{c}^{2}}{2{a}^{2}}$=$\frac{{b}^{2}+{c}^{2}}{2bc}$
∵bc=a2=c2-b2
∴b=$\frac{-1+\sqrt{5}}{2}$c
∴$\frac{{S}_{1}}{{S}_{2}}$=$\frac{\sqrt{5}+2}{2}$.
故选:A.
点评 本题考查圆与圆锥曲线的综合,考查双曲线的性质,面积的计算,解题的关键是确定几何量之间的关系.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
4.下列函数中,导函数是奇函数的是( )
| A. | y=sin2x | B. | y=ex | C. | y=lnx | D. | y=(2x)2 |