题目内容
9.已知函数f(x)=|x-a|+2|x+b|(a>0,b>0)的最小值为1.(1)求a+b的值;
(2)求$\frac{1}{a}$+$\frac{2}{b}$的最小值.
分析 (1)讨论当x<-b时,当-b≤x≤a时,当x>a时,去掉绝对值,再由函数的单调性可得f(x)的最小值,即可得到a+b的值;
(2)运用乘1法,可得$\frac{1}{a}$+$\frac{2}{b}$=(a+b)($\frac{1}{a}$+$\frac{2}{b}$)=3+$\frac{b}{a}$+$\frac{2a}{b}$,运用基本不等式即可得到所求最小值.
解答 解:(1)当x<-b时,f(x)=a-x+2(-x-b)=a-2b-3x,
可得f(x)>a+b;
当-b≤x≤a时,f(x)=a-x+2(x+b)=a+2b+x,
可得a+b≤f(x)≤2a+2b;
当x>a时,f(x)=x-a+2x+2b=3x-a+2b,
可得f(x)>2a+2b.
综上可得f(x)的最小值为a+b,
由题意可得a+b=1;
(2)$\frac{1}{a}$+$\frac{2}{b}$=(a+b)($\frac{1}{a}$+$\frac{2}{b}$)=3+$\frac{b}{a}$+$\frac{2a}{b}$
≥3+2$\sqrt{\frac{b}{a}•\frac{2a}{b}}$=3+2$\sqrt{2}$,
当且仅当b=$\sqrt{2}$a,即a=$\sqrt{2}$-1,b=2-$\sqrt{2}$,
取得最小值3+2$\sqrt{2}$.
点评 本题考查绝对值函数的最值的求法,注意运用分类讨论的思想方法,考查解不等式的运用:求最值,注意运用乘1法,考查运算能力,属于中档题和易错题.

练习册系列答案
相关题目
19.已知二次函数f(x)满足f(1+x)=f(2015-x),且f(x)=0有两个实数根x1,x2,则x1+x2等于( )
| A. | 2014 | B. | 2015 | C. | 2016 | D. | 不确定 |
14.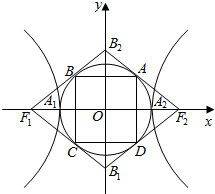 我们把离心率为$\frac{\sqrt{5}+1}{2}$的双曲线叫做黄金双曲线.如图,黄金双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的两顶点为A1,A2,虚轴两端点为B1,B2,两焦点为F1,F2,若以A1,A2为直径的圆内切于菱形F1B1F2B2,切点分别为A,B,C,D,则菱形F1B1F2B2的面积S1与矩形ABCD的面积S2的比值$\frac{{S}_{1}}{{S}_{2}}$=( )
我们把离心率为$\frac{\sqrt{5}+1}{2}$的双曲线叫做黄金双曲线.如图,黄金双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的两顶点为A1,A2,虚轴两端点为B1,B2,两焦点为F1,F2,若以A1,A2为直径的圆内切于菱形F1B1F2B2,切点分别为A,B,C,D,则菱形F1B1F2B2的面积S1与矩形ABCD的面积S2的比值$\frac{{S}_{1}}{{S}_{2}}$=( )
 我们把离心率为$\frac{\sqrt{5}+1}{2}$的双曲线叫做黄金双曲线.如图,黄金双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的两顶点为A1,A2,虚轴两端点为B1,B2,两焦点为F1,F2,若以A1,A2为直径的圆内切于菱形F1B1F2B2,切点分别为A,B,C,D,则菱形F1B1F2B2的面积S1与矩形ABCD的面积S2的比值$\frac{{S}_{1}}{{S}_{2}}$=( )
我们把离心率为$\frac{\sqrt{5}+1}{2}$的双曲线叫做黄金双曲线.如图,黄金双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的两顶点为A1,A2,虚轴两端点为B1,B2,两焦点为F1,F2,若以A1,A2为直径的圆内切于菱形F1B1F2B2,切点分别为A,B,C,D,则菱形F1B1F2B2的面积S1与矩形ABCD的面积S2的比值$\frac{{S}_{1}}{{S}_{2}}$=( )| A. | $\frac{\sqrt{5}+2}{2}$ | B. | $\frac{\sqrt{5}+1}{2}$ | C. | $\frac{\sqrt{5}-2}{2}$ | D. | $\frac{\sqrt{5}-1}{2}$ |
9.已知函数$f(x)=\left\{\begin{array}{l}x,|x|≤1\\ sin\frac{π}{2}x,|x|>1\end{array}\right.$则下列结论正确的是( )
| A. | ?x0∈R,f(-x0)≠-f(x0) | B. | ?x∈R,f(-x)≠f(x) | ||
| C. | 函数f(x)在$[-\frac{π}{2},\frac{π}{2}]$上单调递增 | D. | 函数f(x)的值域是[-1,1] |