10.某中学从高三男生中随机抽取100名学生的身高,将数据整理,得到的频率分布表如下所示.
(Ⅰ)求出频率分布表中①和②位置上相应的数据;
(Ⅱ)为了能对学生的体能做进一步了解,该校决定在第3,4,5组中用分层抽样抽取6名学生进行体能测试,求第3,4,5组每组各抽取多少名学生进行测试?
(Ⅲ)在(Ⅱ)的前提下,学校决定在6名学生中随机抽取2名学生进行引体向上测试,求:第4组中至少有一名学生被抽中的概率.
(Ⅰ)求出频率分布表中①和②位置上相应的数据;
(Ⅱ)为了能对学生的体能做进一步了解,该校决定在第3,4,5组中用分层抽样抽取6名学生进行体能测试,求第3,4,5组每组各抽取多少名学生进行测试?
(Ⅲ)在(Ⅱ)的前提下,学校决定在6名学生中随机抽取2名学生进行引体向上测试,求:第4组中至少有一名学生被抽中的概率.
| 组号 | 分组 | 频数 | 频率 |
| 第1组 | [160,165) | 5 | 0.050 |
| 第2组 | [165,170) | ① | 0.350 |
| 第3组 | [170,175) | 30 | ② |
| 第4组 | [175,180) | 20 | 0.200 |
| 第5组 | [180,185] | 10 | 0.100 |
| 合计 | 100 | 1.00 | |
9.已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<2π)在一个周期内的部分对应值如下表:
(Ⅰ)求f(x)的解析式;
(Ⅱ)求函数g(x)=f(x)+2sinx的最大值和最小值.
| x | $-\frac{π}{2}$ | 0 | $\frac{π}{6}$ | $\frac{π}{2}$ |
| f(x) | -1 | 1 | $\frac{1}{2}$ | -1 |
(Ⅱ)求函数g(x)=f(x)+2sinx的最大值和最小值.
6. 某程序框图如图所示,当输入的x的值为5时,输出的y值恰好是$\frac{1}{3}$,则在空白的处理框处应填入的关系式可以是( )
某程序框图如图所示,当输入的x的值为5时,输出的y值恰好是$\frac{1}{3}$,则在空白的处理框处应填入的关系式可以是( )
 某程序框图如图所示,当输入的x的值为5时,输出的y值恰好是$\frac{1}{3}$,则在空白的处理框处应填入的关系式可以是( )
某程序框图如图所示,当输入的x的值为5时,输出的y值恰好是$\frac{1}{3}$,则在空白的处理框处应填入的关系式可以是( )| A. | y=x3 | B. | y=3x | C. | y=3x | D. | $y=\frac{3}{x}$ |
5.“sin2α-$\sqrt{3}$cos2α=1”是“α=$\frac{π}{4}$”的( )
0 224699 224707 224713 224717 224723 224725 224729 224735 224737 224743 224749 224753 224755 224759 224765 224767 224773 224777 224779 224783 224785 224789 224791 224793 224794 224795 224797 224798 224799 224801 224803 224807 224809 224813 224815 224819 224825 224827 224833 224837 224839 224843 224849 224855 224857 224863 224867 224869 224875 224879 224885 224893 266669
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
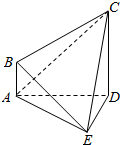 如图,在四棱锥E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=3AB.
如图,在四棱锥E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=3AB.