Question

11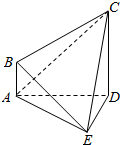．如图，在四棱锥E-ABCD中，AE⊥DE，CD⊥平面ADE，AB⊥平面ADE，CD=3AB．
（Ⅰ）求证：平面ACE⊥平面CDE；
（Ⅱ）在线段DE上是否存在一点F，使AF∥平面BCE？若存在，求出$\frac{EF}{ED}$的值；若不存在，说明理由．

Answer 1

分析 （Ⅰ）证明CD⊥AE．结合AE⊥DE，推出以AE⊥平面CDE．然后证明平面ACE⊥平面CDE．
（Ⅱ）证明：设F为线段DE上一点，且$\frac{EF}{ED}=\frac{1}{3}$．过点F作FM∥CD交CE于M，证明CD∥AB．推出FM∥AB．AF∥BM．即可证明AF∥平面BCE．

解答 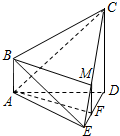（共13分）
证明：（Ⅰ）因为CD⊥平面ADE，AE?平面ADE，
所以CD⊥AE．
又因为AE⊥DE，CD∩DE=D，
所以AE⊥平面CDE．
又因为AE?平面ACE，
所以平面ACE⊥平面CDE．…（7分）
（Ⅱ）在线段DE上存在一点F，且$\frac{EF}{ED}=\frac{1}{3}$，使AF∥平面BCE．
设F为线段DE上一点，且$\frac{EF}{ED}=\frac{1}{3}$．
过点F作FM∥CD交CE于M，则$FM=\frac{1}{3}CD$．
因为CD⊥平面ADE，AB⊥平面ADE，
所以CD∥AB．
又FM∥CD，
所以FM∥AB．
因为CD=3AB，所以FM=AB．
所以四边形ABMF是平行四边形．
所以AF∥BM．
又因为AF?平面BCE，BM?平面BCE，
所以AF∥平面BCE．…（13分）

点评 本题考查直线与平面的位置关系，平面与平面的位置关系的应用，考查逻辑推理能力．