12．甲、乙两名运动员在某项测试中的6次成绩的茎叶图如图所示，${\overline{x}}_{1}$，${\overline{x}}_{2}$分别表示甲、乙两名运动员这项测试成绩的平均数，s${\;}_{1}^{2}$，s${\;}_{2}^{2}$分别表示甲、乙两名运动员这项测试成绩的方差，则有（ ）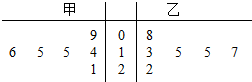
| A． | ${\overline{x}}_{1}$＞${\overline{x}}_{2}$，s${\;}_{1}^{2}$＜${s}_{2}^{2}$ | B． | ${\overline{x}}_{1}$=${\overline{x}}_{2}$，s${\;}_{1}^{2}$＞${s}_{2}^{2}$ | ||
| C． | ${\overline{x}}_{1}$=${\overline{x}}_{2}$，s${\;}_{1}^{2}$=${s}_{2}^{2}$ | D． | ${\overline{x}}_{1}$=${\overline{x}}_{2}$，s${\;}_{1}^{2}$＜${s}_{2}^{2}$ |
11．（1）某社区有500户家庭，其中高收入家庭125户，中等收入家庭280户，低收入家庭95户，为了了解社会购买力的某种指标，要从中抽取一个容量为100户的样本；
（2）从10名同学中抽取3人参加座谈会．
a简单随机抽样 b系统抽样 c分层抽样
问题与方法配对正确的是 （ ）
（2）从10名同学中抽取3人参加座谈会．
a简单随机抽样 b系统抽样 c分层抽样
问题与方法配对正确的是 （ ）
| A． | （1）a，（2）c | B． | （1）a，（2）b | C． | （1）c，（2）a | D． | （1）c，（2）b |
已知函数$f（x）=2sin（{2x-\frac{π}{3}}）$．
4．某地随着经济的发展，居民收入逐年增长，如表是该地一建设银行连续五年的储蓄存款（年底余额），如下表：
为了研究计算的方便，工作人员将上表的数据进行了处理，t=x-2010，z=y-5得到如下表：
（Ⅰ）求z关于t的线性回归方程；
（Ⅱ）通过（Ⅰ）中的方程，求出y关于x的回归方程；
（Ⅲ）用所求回归方程预测到2020年年底，该地储蓄存款额可达多少？
（附：对于线性回归方程$\hat y=\hat bx+\hat a$，其中：$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$）
0 224691 224699 224705 224709 224715 224717 224721 224727 224729 224735 224741 224745 224747 224751 224757 224759 224765 224769 224771 224775 224777 224781 224783 224785 224786 224787 224789 224790 224791 224793 224795 224799 224801 224805 224807 224811 224817 224819 224825 224829 224831 224835 224841 224847 224849 224855 224859 224861 224867 224871 224877 224885 266669
| 年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
| 储蓄存款y（千亿元） | 5 | 6 | 7 | 8 | 10 |
| 时间代号t | 1 | 2 | 3 | 4 | 5 |
| z | 0 | 1 | 2 | 3 | 5 |
（Ⅱ）通过（Ⅰ）中的方程，求出y关于x的回归方程；
（Ⅲ）用所求回归方程预测到2020年年底，该地储蓄存款额可达多少？
（附：对于线性回归方程$\hat y=\hat bx+\hat a$，其中：$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$）