题目内容
7.已知$sinα+cosα=\frac{{3\sqrt{5}}}{5}$,$α∈({\frac{π}{4},\frac{π}{2}})$,求下列各式的值:(1)$\frac{2sinα-3cosα}{4sinα-9cosα}$;
(2)sin2α-3sinαcosα+1.
分析 由条件利用同角三角函数的基本关系,求得sinα 和cosα 的值,从而求得要求式子的值.
解答 解:∵已知$sinα+cosα=\frac{{3\sqrt{5}}}{5}$,$α∈({\frac{π}{4},\frac{π}{2}})$,sin2α+cos2α=1,
∴sinα=$\frac{2\sqrt{5}}{5}$,cosα=$\frac{\sqrt{5}}{5}$,
∴(1)$\frac{2sinα-3cosα}{4sinα-9cosα}$=$\frac{\frac{\sqrt{5}}{5}}{-\frac{\sqrt{5}}{5}}$=-1;
(2)sin2α-3sinαcosα+1=$\frac{20}{25}$-3•$\frac{2\sqrt{5}}{5}$•$\frac{\sqrt{5}}{5}$+1=$\frac{3}{5}$.
点评 本题主要考查同角三角函数的基本关系,属于基础题.

练习册系列答案
相关题目
12.甲、乙两名运动员在某项测试中的6次成绩的茎叶图如图所示,${\overline{x}}_{1}$,${\overline{x}}_{2}$分别表示甲、乙两名运动员这项测试成绩的平均数,s${\;}_{1}^{2}$,s${\;}_{2}^{2}$分别表示甲、乙两名运动员这项测试成绩的方差,则有( )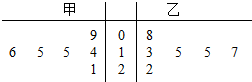

| A. | ${\overline{x}}_{1}$>${\overline{x}}_{2}$,s${\;}_{1}^{2}$<${s}_{2}^{2}$ | B. | ${\overline{x}}_{1}$=${\overline{x}}_{2}$,s${\;}_{1}^{2}$>${s}_{2}^{2}$ | ||
| C. | ${\overline{x}}_{1}$=${\overline{x}}_{2}$,s${\;}_{1}^{2}$=${s}_{2}^{2}$ | D. | ${\overline{x}}_{1}$=${\overline{x}}_{2}$,s${\;}_{1}^{2}$<${s}_{2}^{2}$ |
19.1337与382的最大公约数是( )
| A. | 191 | B. | 382 | C. | 201 | D. | 37 |