题目内容
6.设全集U=R,集合$A=\left\{{x\left|{{{log}_{\frac{1}{2}}}({{x^2}-9x+19})≤0}\right.}\right\}$,$B=\left\{{x\left|{\frac{1}{4}<{2^x}≤32}\right.}\right\}$.(1)求A,B,(∁UA)∩B;
(2)已知C={x|a≤x<a+1},若B∪C=C,求实数a的取值范围.
分析 (1)分别求解对数不等式和指数不等式化简集合A,B,然后利用补集和交集运算求得(∁UA)∩B;
(2)由B∪C=C,得B⊆C,然后利用两集合端点值间的关系列不等式组求得实数a的取值范围.
解答 解:(1)由$lo{g}_{\frac{1}{2}}({x}^{2}-9x+19)≤0$,得x2-9x+19≥1,
即x2-9x+18≥0,解得x≤3或x≥6.
∴A={x|x≤3或x≥6};
由$\frac{1}{4}<{2}^{x}≤32$,解得:-2<x≤5.
∴B={x|-2<x≤5};
∴∁UA={x|3<x<6},
(∁UA)∩B={x|3<x≤5};
(2)C={x|a≤x<a+1},
若B∪C=C,则B⊆C,
得$\left\{\begin{array}{l}{a≤-2}\\{a+1>5}\end{array}\right.$,解得a∈∅.
点评 本题考查对数不等式和指数不等式的解法,考查了交、并、补集的混合运算,考查集合间的包含关系及其应用,关键是对两集合端点值间的关系的处理,是中档题.

练习册系列答案
相关题目
11.(1)某社区有500户家庭,其中高收入家庭125户,中等收入家庭280户,低收入家庭95户,为了了解社会购买力的某种指标,要从中抽取一个容量为100户的样本;
(2)从10名同学中抽取3人参加座谈会.
a简单随机抽样 b系统抽样 c分层抽样
问题与方法配对正确的是 ( )
(2)从10名同学中抽取3人参加座谈会.
a简单随机抽样 b系统抽样 c分层抽样
问题与方法配对正确的是 ( )
| A. | (1)a,(2)c | B. | (1)a,(2)b | C. | (1)c,(2)a | D. | (1)c,(2)b |
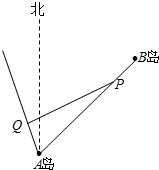 已知海岛B在海岛A的北偏东45°的方向上,两岛相距10海里.小船P从海岛B以2海里/小时的速度沿直线向海岛A移动,同时小船Q从海岛A出发,沿北偏西15°方向以4海里/小时的速度移动.
已知海岛B在海岛A的北偏东45°的方向上,两岛相距10海里.小船P从海岛B以2海里/小时的速度沿直线向海岛A移动,同时小船Q从海岛A出发,沿北偏西15°方向以4海里/小时的速度移动. 已知长方体ABCD-A1B1C1D1,P为棱A1B1上一点,BC=10,CD=10,CC1=4,则AP+PC1的最小值为$2\sqrt{74}$.
已知长方体ABCD-A1B1C1D1,P为棱A1B1上一点,BC=10,CD=10,CC1=4,则AP+PC1的最小值为$2\sqrt{74}$.