题目内容
10.复数$\frac{1-3i}{1-i}$的共轭复数是2+i.分析 利用复数的除法的运算法则化简复数,求出共轭复数即可.
解答 解:复数$\frac{1-3i}{1-i}$=$\frac{(1-3i)(1+i)}{(1-i)(1+i)}$=$\frac{4-2i}{2}$=2-i.
复数的共轭复数为2+i.
故答案为:2+i
点评 本题考查复数的代数形式的混合运算,复数的基本概念的应用,是基础题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
15.已知函数f(x)满足:当f(x)=$\left\{\begin{array}{l}{(\frac{1}{2})^x}\\ f(x+1)\end{array}\right.{,^{\;}}$$\begin{array}{l}x≥4\\ \\ x<4\end{array}$,则f(2+log23)=( )
| A. | $\frac{1}{24}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{8}$ | D. | $\frac{3}{8}$ |
19.已知θ是△ABC的一个内角,且sinθ+cosθ=$\frac{3}{4}$,则方程x2sinθ-y2cosθ=1表示( )
| A. | 焦点在x轴上的双曲线 | B. | 焦点在y轴上的双曲线 | ||
| C. | 焦点在x轴上的椭圆 | D. | 焦点在y轴上的椭圆 |

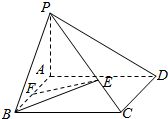 如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,且BE⊥PC于E,PA=a,$BE=\frac{{\sqrt{6}}}{3}a$,点F在线段AB上,并有EF∥平面PAD.则$\frac{BF}{FA}$=$\frac{1}{2}$.
如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,且BE⊥PC于E,PA=a,$BE=\frac{{\sqrt{6}}}{3}a$,点F在线段AB上,并有EF∥平面PAD.则$\frac{BF}{FA}$=$\frac{1}{2}$.