15.$\frac{tan(3π-α)}{{sin(π-α)sin(\frac{3π}{2}-α)}}+\frac{{sin(2π-α)cos(α-\frac{7π}{2})}}{{sin(\frac{3π}{2}+α)cos(2π+α)}}$化简的结果是( )
| A. | -1 | B. | 1 | C. | 0 | D. | $\frac{1}{{{{cos}^2}α}}$ |
14.有一段演绎推理是这样的:“若对数函数y=logax是增函数,已知y=${log_{\frac{1}{4}}}x$是对数函数,则y=${log_{\frac{1}{4}}}x$是增函数”
以上推理的错误是( )
以上推理的错误是( )
| A. | 大前提错误导致结论错误 | B. | 小前提错误导致结论错误 | ||
| C. | 推理形式错误导致结论错误 | D. | 大前提和小前提错误导致结论错误 |
13.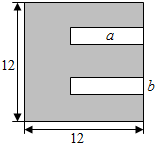 如图所示:一张正方形状的黑色硬质板,剪去两个一样的小矩形得到一个“E”形的图形,设小矩形的长、宽分别为a,b(2≤a≤10),剪去部分的面积为8,则$\frac{1}{b+1}$+$\frac{9}{a+9}$的最大值为( )
如图所示:一张正方形状的黑色硬质板,剪去两个一样的小矩形得到一个“E”形的图形,设小矩形的长、宽分别为a,b(2≤a≤10),剪去部分的面积为8,则$\frac{1}{b+1}$+$\frac{9}{a+9}$的最大值为( )
 如图所示:一张正方形状的黑色硬质板,剪去两个一样的小矩形得到一个“E”形的图形,设小矩形的长、宽分别为a,b(2≤a≤10),剪去部分的面积为8,则$\frac{1}{b+1}$+$\frac{9}{a+9}$的最大值为( )
如图所示:一张正方形状的黑色硬质板,剪去两个一样的小矩形得到一个“E”形的图形,设小矩形的长、宽分别为a,b(2≤a≤10),剪去部分的面积为8,则$\frac{1}{b+1}$+$\frac{9}{a+9}$的最大值为( )| A. | 1 | B. | $\frac{11}{10}$ | C. | $\frac{6}{5}$ | D. | 2 |
12.一个几何体的三视图如图所示,则这个几何体外接球的体积为( )
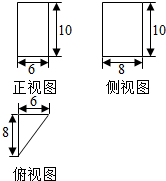

| A. | 1000$\sqrt{2}$π | B. | 200π | C. | $\frac{200}{3}$π | D. | $\frac{1000\sqrt{2}}{3}$π |
11.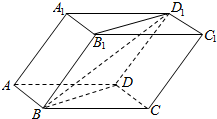 已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则异面直线BD1与AA1所成的角的余弦值为( )
已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则异面直线BD1与AA1所成的角的余弦值为( )
 已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则异面直线BD1与AA1所成的角的余弦值为( )
已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则异面直线BD1与AA1所成的角的余弦值为( )| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{13}}{4}$ | C. | $\frac{\sqrt{39}}{13}$ | D. | $\frac{3}{4}$ |
10.在△ABC中,a=4,b=$\frac{5}{2}$,cos(A-B)cosB-sin(A-B)sin(A+C)=$\frac{3}{5}$,则角B的大小为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{6}$ |
9.设Sn为等比数列{an}的前n项和,记命题甲:4a2-a4=0,命题乙:S4=5S2,则命题甲成立是命题乙成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
8.将函数y=sin(2x+$\frac{π}{3}$)的图象向右平移φ(0<φ<$\frac{π}{2}$)个单位后的图象关于y轴对称,则φ=( )
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
7.复数$\frac{i}{1-2i}$(i为虚数单位)的共轭复数为( )
0 224111 224119 224125 224129 224135 224137 224141 224147 224149 224155 224161 224165 224167 224171 224177 224179 224185 224189 224191 224195 224197 224201 224203 224205 224206 224207 224209 224210 224211 224213 224215 224219 224221 224225 224227 224231 224237 224239 224245 224249 224251 224255 224261 224267 224269 224275 224279 224281 224287 224291 224297 224305 266669
| A. | $\frac{-2+i}{5}$ | B. | $\frac{-2-i}{5}$ | C. | $\frac{2-i}{5}$ | D. | $\frac{2+i}{5}$ |