题目内容
13.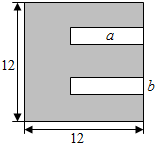 如图所示:一张正方形状的黑色硬质板,剪去两个一样的小矩形得到一个“E”形的图形,设小矩形的长、宽分别为a,b(2≤a≤10),剪去部分的面积为8,则$\frac{1}{b+1}$+$\frac{9}{a+9}$的最大值为( )
如图所示:一张正方形状的黑色硬质板,剪去两个一样的小矩形得到一个“E”形的图形,设小矩形的长、宽分别为a,b(2≤a≤10),剪去部分的面积为8,则$\frac{1}{b+1}$+$\frac{9}{a+9}$的最大值为( )| A. | 1 | B. | $\frac{11}{10}$ | C. | $\frac{6}{5}$ | D. | 2 |
分析 由题意,2ab=8,b=$\frac{4}{a}$,从而将问题转化为关于a的函数,利用基本不等式,即可得出结论.
解答 解:由题意,2ab=8,∴b=$\frac{4}{a}$,
∵2≤a≤10,
∴$\frac{1}{b+1}$+$\frac{9}{a+9}$=$\frac{1}{\frac{4}{a}+1}$+$\frac{9}{a+9}$=1+$\frac{5}{a+\frac{36}{a}+13}$$≤1+\frac{5}{13+2\sqrt{a•\frac{36}{a}}}$=$\frac{6}{5}$,
当且仅当a=$\frac{36}{a}$,即a=6时,$\frac{1}{b+1}$+$\frac{9}{a+9}$的最大值为$\frac{6}{5}$,
故选:C.
点评 本题考查利用数学知识解决实际问题,考查基本不等式的运用,正确转化是关键.

练习册系列答案
相关题目
4.设命题p:?x0∈(0,+∞),e${\;}^{{x}_{0}}$+x0=5.命题q:?x∈(0,+∞),$\frac{3}{x+1}$+x≥2$\sqrt{3}$-1.那么,下列命题为真命题的是( )
| A. | ¬q | B. | (¬p)∨(¬q) | C. | p∧q | D. | p∧(¬q) |
1.已知f(x)=$\left\{\begin{array}{l}{{x}^{2},x>0}\\{π,x=0}\\{0,x<0}\end{array}\right.$,则f(-π)等于( )
| A. | 0 | B. | 9 | C. | π2 | D. | π |
8.将函数y=sin(2x+$\frac{π}{3}$)的图象向右平移φ(0<φ<$\frac{π}{2}$)个单位后的图象关于y轴对称,则φ=( )
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
2.函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-2,x≤1}\\{-lo{g}_{2}(x+1),x>1}\end{array}\right.$且f(a)=-3,则f(5-a)=( )
| A. | -$\frac{7}{4}$ | B. | -$\frac{5}{4}$ | C. | -$\frac{3}{4}$ | D. | -$\frac{1}{4}$ |
3.奇函数f(x)在(0,+∞)上递增,且f(-2)=0,则不等式 $\frac{f(x)-f(-x)}{x}$<0的解集为( )
| A. | (-∞,-2)∪(0,2) | B. | (-2,0)∪(0,2) | C. | (-∞,-2)∪(2,+∞) | D. | (-2,0)∪(2,+∞) |