题目内容
8.将函数y=sin(2x+$\frac{π}{3}$)的图象向右平移φ(0<φ<$\frac{π}{2}$)个单位后的图象关于y轴对称,则φ=( )| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
分析 利用三角函数的图象平移得到y=sin(2x-2φ+$\frac{π}{3}$),结合该函数为偶函数,及φ的范围即可求得φ的值.
解答 解:∵函数y=sin(2x+$\frac{π}{3}$)的图象向右平移φ(0<φ<$\frac{π}{2}$)个单位后的解析式为:y=sin[2(x-φ)+$\frac{π}{3}$]=sin(2x-2φ+$\frac{π}{3}$),
∵其图象关于y轴对称,
∴-2φ+$\frac{π}{3}$=k$π+\frac{π}{2}$,k∈Z,
∴解得:φ=-$\frac{kπ}{2}-\frac{π}{12}$,k∈Z,
∵0<φ<$\frac{π}{2}$
∴φ=$\frac{5π}{12}$.
故选:D.
点评 本题考查了三角函数的图象平移,考查了三角函数奇偶性的性质,是基础题.

练习册系列答案
相关题目
9.满足条件|z-i|2+|z+4|2=9的复数z在复平面上对应点的轨迹是( )
| A. | 一条直线 | B. | 圆 | C. | 椭圆 | D. | 双曲线 |
16.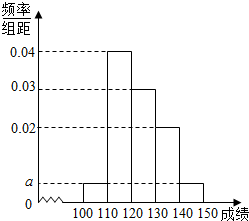 贵阳市某中学高三第一次摸底考试中100名学生数学成绩的频率分布直方图如图所示,其中成绩分组区间是[100,110),[110,120),[120,130),[130,140),[140,150].
贵阳市某中学高三第一次摸底考试中100名学生数学成绩的频率分布直方图如图所示,其中成绩分组区间是[100,110),[110,120),[120,130),[130,140),[140,150].
(Ⅰ)求图中a的值;
(Ⅱ)根据频率分布直方图,估计这100名学生数学成绩的平均分;
(Ⅲ)若这100名学生数学成绩某些分数段的人数(x)与语文成绩相应分数段的人数(y)之比如下表所示,求语文成绩在[100,140)之外的人数.
 贵阳市某中学高三第一次摸底考试中100名学生数学成绩的频率分布直方图如图所示,其中成绩分组区间是[100,110),[110,120),[120,130),[130,140),[140,150].
贵阳市某中学高三第一次摸底考试中100名学生数学成绩的频率分布直方图如图所示,其中成绩分组区间是[100,110),[110,120),[120,130),[130,140),[140,150].(Ⅰ)求图中a的值;
(Ⅱ)根据频率分布直方图,估计这100名学生数学成绩的平均分;
(Ⅲ)若这100名学生数学成绩某些分数段的人数(x)与语文成绩相应分数段的人数(y)之比如下表所示,求语文成绩在[100,140)之外的人数.
| 分数段 | [100,110) | [110,120) | [120,130) | [130,140) |
| x:y | 1:1 | 2:1 | 3:4 | 4:5 |
3.函数$f(x)=sin(x+\frac{π}{6})cos(x+\frac{π}{6})$,给出下列结论正确的是( )
| A. | f(x)的最小正周期为 $\frac{π}{2}$ | B. | f(x)的一条对称轴为$x=\frac{π}{6}$ | ||
| C. | f(x)的一个对称中心为$(\frac{π}{6},0)$ | D. | $f(x-\frac{π}{6})$是奇函数 |
13.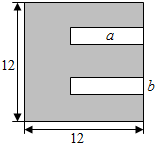 如图所示:一张正方形状的黑色硬质板,剪去两个一样的小矩形得到一个“E”形的图形,设小矩形的长、宽分别为a,b(2≤a≤10),剪去部分的面积为8,则$\frac{1}{b+1}$+$\frac{9}{a+9}$的最大值为( )
如图所示:一张正方形状的黑色硬质板,剪去两个一样的小矩形得到一个“E”形的图形,设小矩形的长、宽分别为a,b(2≤a≤10),剪去部分的面积为8,则$\frac{1}{b+1}$+$\frac{9}{a+9}$的最大值为( )
 如图所示:一张正方形状的黑色硬质板,剪去两个一样的小矩形得到一个“E”形的图形,设小矩形的长、宽分别为a,b(2≤a≤10),剪去部分的面积为8,则$\frac{1}{b+1}$+$\frac{9}{a+9}$的最大值为( )
如图所示:一张正方形状的黑色硬质板,剪去两个一样的小矩形得到一个“E”形的图形,设小矩形的长、宽分别为a,b(2≤a≤10),剪去部分的面积为8,则$\frac{1}{b+1}$+$\frac{9}{a+9}$的最大值为( )| A. | 1 | B. | $\frac{11}{10}$ | C. | $\frac{6}{5}$ | D. | 2 |



