题目内容
6.已知点(sin$\frac{nπ}{2}$,an+$\frac{\sqrt{2}π}{4}$)在直线l:y=-$\sqrt{2}$x+$\frac{\sqrt{2}π}{4}$+2$\sqrt{2}$上,则数列{an}的前30项的和为59$\sqrt{2}$.分析 把点(sin$\frac{nπ}{2}$,an+$\frac{\sqrt{2}π}{4}$)代入直线l,得an=2$\sqrt{2}$-$\sqrt{2}$sin$\frac{nπ}{2}$,由sin$\frac{nπ}{2}$的取值是1,0,-1,0的循环,能求出数列{an}的前30项和.
解答 解:点(sin$\frac{nπ}{2}$,an+$\frac{\sqrt{2}π}{4}$)在直线l:y=-$\sqrt{2}$x+$\frac{\sqrt{2}π}{4}$+2$\sqrt{2}$上,
∴an=2$\sqrt{2}$-$\sqrt{2}$sin$\frac{nπ}{2}$,
sin$\frac{nπ}{2}$的最小正周期为4,取值是1,0,-1,0的循环,
∴数列{an}的前30项和:
S30=30×2$\sqrt{2}$-$\sqrt{2}$[7(1+0-1+0)+1+0]=59$\sqrt{2}$.
故答案为:59$\sqrt{2}$.
点评 本题考查数列的前30项和的求法,是中档题,解题时要注意三角函数的周期性的合理运用.

练习册系列答案
相关题目
14.已知集合 P={x||x|>x},$Q=\left\{{x\left|{y=\sqrt{1-x}}\right.}\right\}$,则 P∩Q=( )
| A. | (-∞,0) | B. | (0,1] | C. | (-∞,1] | D. | [0,1] |
1.已知f(x)=$\left\{\begin{array}{l}{{x}^{2},x>0}\\{π,x=0}\\{0,x<0}\end{array}\right.$,则f(-π)等于( )
| A. | 0 | B. | 9 | C. | π2 | D. | π |
11.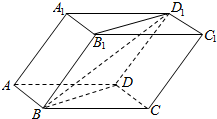 已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则异面直线BD1与AA1所成的角的余弦值为( )
已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则异面直线BD1与AA1所成的角的余弦值为( )
 已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则异面直线BD1与AA1所成的角的余弦值为( )
已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则异面直线BD1与AA1所成的角的余弦值为( )| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{13}}{4}$ | C. | $\frac{\sqrt{39}}{13}$ | D. | $\frac{3}{4}$ |
15.已知:对任意x∈[0,1]都有$\sqrt{1-{x^2}}-cosωx≥0$成立,且ω>0则ω的取值范围为( )
| A. | $[\frac{π}{4},\frac{π}{2}]$ | B. | $(\frac{π}{4},\frac{π}{2}]$ | C. | $[\frac{π}{2},\frac{3π}{2}]$ | D. | $[\frac{π}{2},\frac{3π}{2})$ |