先后两次抛掷一枚骰子，在得到的点数中有3的概率为（　　）
A、
1
3
B、
1
4
C、
11
36
D、
13
36
下列结论中，正确的是（　　）
A、“?x∈Q，x2-5=0”的否定是假命题
B、“?x∈R，x2+1＜1”的否定是“?x∈R，x2+1＜1”
C、“2≤2”是真命题
D、“?x∈R，x2+1≠0”的否定是真命题
在平面直角坐标系中，O为坐标原点，点A（2，0），将向量
OA
绕点O按逆时针方向旋转
π
3
后得向量
OB
，若向量
a
满足|
a
-
OA
-
OB
|=1，则|
a
|的最大值是（　　）
A、2
3
-1
B、2
3
+1
C、3
D、
6
+
2
+1
从2、3、5、7这四个质数中任取两个相乘，可以得到不相等的积的个数是（　　）
A、4B、5C、6D、8
已知全集U={x∈Z|1≤x≤5}，A={1，2，3}，∁UB={1，2}，则A∩B（　　）
A、{1，2}
B、{1，3}
C、{3}
D、{1，2，3}
条件p：x≥0，条件q：x2≤x，则p是q的（　　）
A、充分而不必要条件
B、必要而不充分条件
C、充要条件
D、既不充分也不必要条件
下列说法错误的是（　　）
A、若命题p：?x∈R，x2-x+1=0，则￢p：?x∈R，x2-x+1≠0
B、若命题p：?x∈R，cosx=1，q：?x∈R，x2-x+1＞0，则“p∧￢q”为假命题．
C、命题“若a=0，则ab=0”的否命题是：“若a≠0，则ab≠0”
D、“sinθ=
1
2
”是“θ=30°”的充分不必要条件
复数z=
1-i
2+i
在复平面上对应的点的坐标为（　　）
A、(
1
5
，-
1
5
)
B、(
3
5
，-
1
5
)
C、(
1
5
，
1
5
)
D、(
1
5
，-
3
5
)
等比数列{an}满足an＞0，n∈N+，且a3•a2n-3=22n(n≥2)，则当n≥1时，log2a1+log2a2+…+log2a2n-1=（　　）
A、n（2n-1）
B、（n+1）2
C、n2
D、（n-1）2
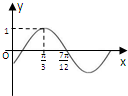已知函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜
π
2
）的部分图象如图所示，则y=f（x+
π
6
）取得最小值时x的集合为（　　）
A、{x|x=kπ-
π
6
，k∈Z }
B、{x|x=kπ-
π
3
，k∈Z }
C、{x|x=2kπ-
π
6
，k∈Z }
D、{x|x=2kπ-
π
3
，k∈Z }
 0  212765  212773  212779  212783  212789  212791  212795  212801  212803  212809  212815  212819  212821  212825  212831  212833  212839  212843  212845  212849  212851  212855  212857  212859  212860  212861  212863  212864  212865  212867  212869  212873  212875  212879  212881  212885  212891  212893  212899  212903  212905  212909  212915  212921  212923  212929  212933  212935  212941  212945  212951  212959  266669 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网