题目内容
在平面直角坐标系中,O为坐标原点,点A(2,0),将向量
绕点O按逆时针方向旋转
后得向量
,若向量
满足|
-
-
|=1,则|
|的最大值是( )
| OA |
| π |
| 3 |
| OB |
| a |
| a |
| OA |
| OB |
| a |
A、2
| ||||
B、2
| ||||
| C、3 | ||||
D、
|
考点:平面向量数量积的运算
专题:平面向量及应用
分析:设
=(x,y),根据|
-
-
|=1 可得 (x-3)2+(y-
)2=1,故(x,y)在以M(3,
)为圆心,以1为半径的圆上,再根据|
|=
的最大值为|0M|+r,计算求得结果.
| a |
| a |
| OA |
| OB |
| 3 |
| 3 |
| a |
| x2+y2 |
解答:
解:由题意可得点B(1,
),设
=(x,y),则
-
-
=(x-3,y-
),
由|
-
-
|=1 可得 (x-3)2+(y-
)2=1,
故(x,y)在以M(3,
)为圆心,以1为半径的圆上,
再根据|OM|=2
,可得|
|=
的最大值为|0M|+r=2
+1,
故选:B.
| 3 |
| a |
| a |
| OA |
| OB |
| 3 |
由|
| a |
| OA |
| OB |
| 3 |
故(x,y)在以M(3,
| 3 |
再根据|OM|=2
| 3 |
| a |
| x2+y2 |
| 3 |
故选:B.
点评:本题主要考查两个向量的数量积的运算,求向量的模,属于中档题.

练习册系列答案
相关题目
已知集合A={x|x2-5x-6<0},B={x||x|<2},则A∩(∁RB)=( )
| A、(-1,2) |
| B、[-1,2) |
| C、(2,6) |
| D、[2,6) |
复数z=
在复平面上对应的点的坐标为( )
| 1-i |
| 2+i |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
若函数y=cosωx(ω>0)的图象向右平移
个单位后与函数y=sinωx的图象重合,则ω的值可能是( )
| π |
| 6 |
A、
| ||
| B、1 | ||
| C、3 | ||
| D、4 |
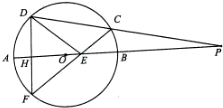 已知:如图,P是⊙O的直径AB延长线上的一点,割线PCD交⊙O于C、D两点,弦DF与直线AB垂直,H为垂足,CF与AB交于点E.
已知:如图,P是⊙O的直径AB延长线上的一点,割线PCD交⊙O于C、D两点,弦DF与直线AB垂直,H为垂足,CF与AB交于点E.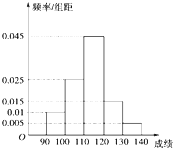 某校高三数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示.若130~140分数段的人数为2人.
某校高三数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示.若130~140分数段的人数为2人.