题目内容
先后两次抛掷一枚骰子,在得到的点数中有3的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:古典概型及其概率计算公式
专题:概率与统计
分析:本题的关键是写出基本事件空间Ω,以及写出“得到的点数中有3”这个事件A,根据古典概型的计算公式,得到概率P(A)
解答:
解:Ω={(1,1),(1,2),(1,3),(1,4),(1,5),(1,6)
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6)
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6)
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)}
基本事件空间所含基本事件的个数:n(Ω)=36
设得到的点数中有3”这个事件为A
A={ (1,3),(2,3),(3,1),(3,2),(3,3),(3,4),(3,5),(3,6)
(4,3),(5,3),(6,3)}
事件A所含基本事件的个数:n(A)=11
根据古典概型的计算公式:P(A)=
=
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6)
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6)
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)}
基本事件空间所含基本事件的个数:n(Ω)=36
设得到的点数中有3”这个事件为A
A={ (1,3),(2,3),(3,1),(3,2),(3,3),(3,4),(3,5),(3,6)
(4,3),(5,3),(6,3)}
事件A所含基本事件的个数:n(A)=11
根据古典概型的计算公式:P(A)=
| n(A) |
| n(Ω) |
| 11 |
| 36 |
点评:本题考查古典概型的计算方法,是一道基础题目

练习册系列答案
相关题目
已知实数x,y满足方程(x-2)2+y2=1,那么
的最大值为( )
| y |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
条件p:x≥0,条件q:x2≤x,则p是q的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
 如图,已知动圆M过定点F(0,1)且与x轴相切,点F关于圆心M的对称点为F′,动点F′的轨迹为C.
如图,已知动圆M过定点F(0,1)且与x轴相切,点F关于圆心M的对称点为F′,动点F′的轨迹为C.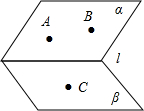 如图,已知平面α∩β=l,点A∈α,点B∈α,点C属于β,且A∉l,B∉l,直线AB与l不平行,那么平面ABC与平面β的交线与l有什么关系?证明你的结论.
如图,已知平面α∩β=l,点A∈α,点B∈α,点C属于β,且A∉l,B∉l,直线AB与l不平行,那么平面ABC与平面β的交线与l有什么关系?证明你的结论.