题目内容
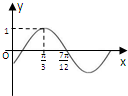 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<| π |
| 2 |
| π |
| 6 |
A、{x|x=kπ-
| ||
B、{x|x=kπ-
| ||
C、{x|x=2kπ-
| ||
D、{x|x=2kπ-
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:根据函数的图象,求出A,T,利用周期公式求出ω,结合函数图象过(6,0)以及|φ|<
,求出ϕ的值.得到函数的解析式.
| π |
| 2 |
解答:
 解:由题意可知A=1,T=4×(
解:由题意可知A=1,T=4×(
-
)=π,∴ω=
=2,
∵函数经过(
,0),
∴0=2sin(2×
+φ),∵|φ|<
,∴φ=-
,
∴函数的解析式为:y=sin(2x-
).
故函数的解析式.y=f(x+
)=sin(2x+
).x∈R.
函数取得最小值时2x+
=2kπ-
,k∈Z.解得x=kπ-
,k∈Z.
故选:B.
 解:由题意可知A=1,T=4×(
解:由题意可知A=1,T=4×(| 7π |
| 12 |
| π |
| 3 |
| 2π |
| π |
∵函数经过(
| 7π |
| 12 |
∴0=2sin(2×
| 7π |
| 12 |
| π |
| 2 |
| π |
| 6 |
∴函数的解析式为:y=sin(2x-
| π |
| 6 |
故函数的解析式.y=f(x+
| π |
| 6 |
| π |
| 6 |
函数取得最小值时2x+
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
故选:B.
点评:本题是中档题,考查函数的图象求出函数的解析式的方法,注意视图用图能力的培养.

练习册系列答案
相关题目
下列关于两条不同的直线l,m两个不重合的平面α,β的说法,正确的是( )
| A、若l?α且α⊥β,则l⊥β |
| B、若l⊥β且m⊥β,则l∥m |
| C、若l⊥β且α⊥β,则l∥α |
| D、若α∩β=m且l⊥m,则l⊥α |
已知集合A={x|x2-5x-6<0},B={x||x|<2},则A∩(∁RB)=( )
| A、(-1,2) |
| B、[-1,2) |
| C、(2,6) |
| D、[2,6) |
已知全集U={x∈Z|1≤x≤5},A={1,2,3},∁UB={1,2},则A∩B( )
| A、{1,2} |
| B、{1,3} |
| C、{3} |
| D、{1,2,3} |
若函数y=cosωx(ω>0)的图象向右平移
个单位后与函数y=sinωx的图象重合,则ω的值可能是( )
| π |
| 6 |
A、
| ||
| B、1 | ||
| C、3 | ||
| D、4 |