设f（n）=(
)n-1+(
)n+1（n∈Z），则f（2014）（ ）
| 1+i |
| 1-i |
| 1-i |
| 1+i |
| A、2 | B、-2 | C、2i | D、-2i |
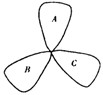荷花池中，有一只青蛙在成品字形的三片荷叶上跳来跳去（每次跳跃时，均从一叶跳到另一叶），而且逆时针方向跳的概率是顺时针方向跳的概率的两倍，如图．假设现在青蛙在A叶上，则跳三次之后停在A叶上的概率是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
定义在R上的函数y=f（x）是减函数，且函数y=f（x-2）的图象关于点（2，0）成中心对称，若m，n满足不等式f（m2-2m）+f（2n-n2）≤0．则当1≤m≤4时，
的取值范围是（ ）
| n |
| m |
A、[-
| ||
B、[-
| ||
C、[-
| ||
D、[-
|
已知一元二次不等式f（x）≤0的解集为{x|x≤
，或x≥3}，则f（ex）＞0的解集为（ ）
| 1 |
| 2 |
| A、{x|x＜-ln2，或x＞ln3} |
| B、{x|ln2＜x＜ln3} |
| C、{x|x＜ln3}} |
| D、{x|-ln2＜x＜ln3} |
等边△ABC的边长为1，过△ABC的中心O作OP⊥平面ABC，且OP=
| ||
| 3 |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
执行如图所示的程序框图，若输入的p=0.8，则输出的n为（ ）
| A、4 | B、5 | C、6 | D、3 |
执行如图所示的程序框图．则输出的所有点（x，y）都在函数（ ）的图象上．| A、y=x+1 |
| B、y=2x |
| C、y=2x |
| D、y=2x-1 |
定义在R上的偶函数f（x）满足f（x+1）f（x）=-2（f（x）≠0），且在区间（2013，2014）上单调递增，已知α，β是锐角三角形的两个内角，则f（sinα）、f（cosβ）的大小关系是（ ）
| A、f（sinα）＜f（cosβ） |
| B、f（sinα）＞f（cosβ） |
| C、f（sinα）=f（cosβ） |
| D、以上情况均有可能 |
（理）椭圆
+
=1上的点到圆（x+6）2+y2=1上的点的距离的最大值（ ）
| x2 |
| 16 |
| y2 |
| 25 |
| A、11 | ||
| B、9 | ||
C、
| ||
D、5
|