题目内容
定义在R上的偶函数f(x)满足f(x+1)f(x)=-2(f(x)≠0),且在区间(2013,2014)上单调递增,已知α,β是锐角三角形的两个内角,则f(sinα)、f(cosβ)的大小关系是( )
| A、f(sinα)<f(cosβ) |
| B、f(sinα)>f(cosβ) |
| C、f(sinα)=f(cosβ) |
| D、以上情况均有可能 |
考点:函数奇偶性的判断
专题:函数的性质及应用
分析:由条件可得f(x)是周期为2的偶函数,在(-1,0)上单调递增,故函数在(0,1)上单调递减.
根据α,β是锐角三角形的两个内角,可得
>α>
-β>0,可得1>sinα>sin(
-β)=cosβ>0.
从而得到f(sinα)与f(cosβ)的大小关系.
根据α,β是锐角三角形的两个内角,可得
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
从而得到f(sinα)与f(cosβ)的大小关系.
解答:
解:∵定义在R上的偶函数f(x)满足f(x+1)f(x)=-2,
∴f(x)=
=
=f(x+2),
∴f(x)是周期为2的偶函数.
∵函数f(x)在区间(2013,2014)上单调递增,
故函数在(-1,0)上单调递增,在(0,1)上单调递减.
∵α,β是锐角三角形的两个内角,∴α+β>
,∴
>α>
-β>0,
∴1>sinα>sin(
-β)=cosβ>0.
则f(sinα)<f(cosβ),
故选:A.
∴f(x)=
| -2 |
| f(x+1) |
| -2 | ||
|
∴f(x)是周期为2的偶函数.
∵函数f(x)在区间(2013,2014)上单调递增,
故函数在(-1,0)上单调递增,在(0,1)上单调递减.
∵α,β是锐角三角形的两个内角,∴α+β>
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
∴1>sinα>sin(
| π |
| 2 |
则f(sinα)<f(cosβ),
故选:A.
点评:本题考查函数的奇偶性和单调性,考查三角函数的单调性,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
正三棱锥P-ABC的高为2,侧棱与底面所成的角为45°,则点A到侧面PBC的距离是( )
A、
| ||||
B、2
| ||||
C、
| ||||
D、
|
已知|
|=1,|
|=2且(
+
)与
垂直,则
与
的夹角是( )
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| A、60° | B、90° |
| C、135° | D、120° |
对于平面α和两条不同的直线m,n,下列命题是真命题的是( )
| A、若m⊥α,n⊥α,则m∥n |
| B、若m∥α,n∥α则m∥n |
| C、若m⊥α,m⊥n则n∥α |
| D、若m,n与α所成的角相等,则m∥n |
已知一元二次不等式f(x)≤0的解集为{x|x≤
,或x≥3},则f(ex)>0的解集为( )
| 1 |
| 2 |
| A、{x|x<-ln2,或x>ln3} |
| B、{x|ln2<x<ln3} |
| C、{x|x<ln3}} |
| D、{x|-ln2<x<ln3} |
已知集合U=R,集合A={x|-l≤x≤3},集合B=|x|log2x<2},则A∩B=( )
| A、{x|1≤x≤3} |
| B、{x|-1≤x≤3} |
| C、{x|0<x≤3} |
| D、{x|-1≤x<0} |

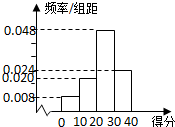 对甲、乙两名篮球运动员分别在100场比赛中的得分情况进行统计,做出甲的得分频率分布直方图如图所示,列出乙的得分统计表如下:
对甲、乙两名篮球运动员分别在100场比赛中的得分情况进行统计,做出甲的得分频率分布直方图如图所示,列出乙的得分统计表如下: