题目内容
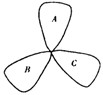 荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图.假设现在青蛙在A叶上,则跳三次之后停在A叶上的概率是( )
荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图.假设现在青蛙在A叶上,则跳三次之后停在A叶上的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
考点:相互独立事件的概率乘法公式
专题:概率与统计
分析:根据条件先求出逆时针和顺时针跳的概率,然后根据跳3次回到A,则应满足3次逆时针或者3次顺时针,根据概率公式即可得到结论.
解答:
解:设按照顺时针跳的概率为p,则逆时针方向跳的概率为2p,则p+2p=3p=1,
解得p=
,即按照顺时针跳的概率为
,则逆时针方向跳的概率为
,
若青蛙在A叶上,则跳3次之后停在A叶上,
则满足3次逆时针或者3次顺时针,
①若先按逆时针开始从A→B,则对应的概率为
×
×
=
,
②若先按顺时针开始从A→C,则对应的概率为
×
×
=
,
则概率为
+
=
=
,
故选:A
解得p=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
若青蛙在A叶上,则跳3次之后停在A叶上,
则满足3次逆时针或者3次顺时针,
①若先按逆时针开始从A→B,则对应的概率为
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 8 |
| 27 |
②若先按顺时针开始从A→C,则对应的概率为
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 27 |
则概率为
| 1 |
| 27 |
| 8 |
| 27 |
| 9 |
| 27 |
| 1 |
| 3 |
故选:A
点评:本题主要考查概率的计算,利用独立重复试验的概率公式是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知∠BAC在平面α内,PA是α的斜线,若∠PAB=∠PAC=∠BAC=60°,PA=a,则点P到平面α的距离为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
对于平面α和两条不同的直线m,n,下列命题是真命题的是( )
| A、若m⊥α,n⊥α,则m∥n |
| B、若m∥α,n∥α则m∥n |
| C、若m⊥α,m⊥n则n∥α |
| D、若m,n与α所成的角相等,则m∥n |
执行如图所示的程序框图,若输入的p=0.8,则输出的n为( )


| A、4 | B、5 | C、6 | D、3 |
已知集合U=R,集合A={x|-l≤x≤3},集合B=|x|log2x<2},则A∩B=( )
| A、{x|1≤x≤3} |
| B、{x|-1≤x≤3} |
| C、{x|0<x≤3} |
| D、{x|-1≤x<0} |