题目内容
已知一元二次不等式f（x）≤0的解集为{x|x≤
，或x≥3}，则f（ex）＞0的解集为（ ）
| 1 |
| 2 |
| A、{x|x＜-ln2，或x＞ln3} |
| B、{x|ln2＜x＜ln3} |
| C、{x|x＜ln3}} |
| D、{x|-ln2＜x＜ln3} |
考点：二次函数的性质
专题：函数的性质及应用
分析：由已知利用补集思想求出一元二次不等式f（x）＞0的解集{x|
＜x＜3}，然后由
＜ex＜3，求解x的取值集合即可得到答案．
| 1 |
| 2 |
| 1 |
| 2 |
解答：
解：∵一元二次不等式f（x）≤0的解集为{x|x≤
，或x≥3}，
∴一元二次不等式f（x）＞0的解集为{x|
＜x＜3}．
由
＜ex＜3，得：-ln2＜x＜ln3．
∴f（ex）＞0的解集为{x|-ln2＜x＜ln3}．
故选：D．
| 1 |
| 2 |
∴一元二次不等式f（x）＞0的解集为{x|
| 1 |
| 2 |
由
| 1 |
| 2 |
∴f（ex）＞0的解集为{x|-ln2＜x＜ln3}．
故选：D．
点评：本题考查了一元二次不等式的解法，训练了补集思想的应用，关键是明确求解f（ex）＞0要保证
＜ex＜3，是中档题．
| 1 |
| 2 |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
长方体ABCD-A1B1C1D1，AB=2，AD=2，AA1=
，则点D到平面ACD1的距离是（ ）
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
定义在R上的偶函数f（x）满足f（x+1）f（x）=-2（f（x）≠0），且在区间（2013，2014）上单调递增，已知α，β是锐角三角形的两个内角，则f（sinα）、f（cosβ）的大小关系是（ ）
| A、f（sinα）＜f（cosβ） |
| B、f（sinα）＞f（cosβ） |
| C、f（sinα）=f（cosβ） |
| D、以上情况均有可能 |
对于平面α，β，γ和直线a，b，m，n，下列命题中真命题是（ ）
| A、若a⊥m，a⊥n，m?α，n?α，则a⊥α |
| B、若α∥β，α∩γ=a，β∩γ=b则a∥b |
| C、若a∥b，b?α，则a∥α |
| D、若a?β，b?β，a∥α，b∥α，则β∥α |
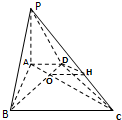如图示，在底面为直角梯形的四棱椎P-ABCD中，AD∥BC，∠ABC=90°，PA⊥平面ABCD，PA=4，AD=2，AB=2
已知an=（