某程序框图如图所示,则该程序运行后输出的S的值为( )


A、
| ||
B、
| ||
C、
| ||
| D、1 |
若复数z=
|z|+
i(i为虚数单位),|z|是z的模,则z的虚部是( )
| 1 |
| 2 |
| 3 |
A、1+
| ||
B、±1+
| ||
| C、1 | ||
D、
|
已知f(x)是定义在R上的奇函数,若对于x≥0,都有f(x+2)=f(x),且当x∈[0,2]时,f(x)=ex-1,则f(2013)+f(-2014)=( )
| A、e-1 | B、1-e |
| C、-1-e | D、e+1 |
已知数列{an }的前n项和为Sn,执行如图的程序框图,则输出的M一定满足( )


| A、Sn=nM | ||
B、Sn=
| ||
| C、Sn≤nM | ||
| D、Sn≥nM |
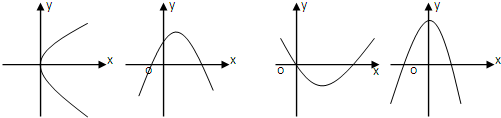
在下面的四个图象中,其中一个图象是函f(x)=
x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)的图象,则f(-1)等于( )
| 1 |
| 3 |

A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知a∈R,若函数f(x)=x2-|2x-a|有四个零点,则关于x的方程ax2+2x+1=0的实数根的个数为( )
| A、2个 | B、1个 |
| C、0个 | D、与a的取值有关 |
已知f1(x)=sinx-cosx,fn+1(x)是fn(x)的导函数,即f2(x)=f1′(x),f3(x)=f2′(x),…,fn+1(x)=fn′(x),n∈N*,则f2014(x)=( )
| A、sinx+cosx |
| B、sinx-cosx |
| C、-sinx+cosx |
| D、-sinx-cosx |
已知a∈{2,3},b∈{1,2,3},执行如图所示程序框图,则输出的结果共有( )


| A、3种 | B、4种 | C、5种 | D、6种 |
阅读如图的程序框图,运行相应的程序,若输出S=42,则判断框内可以填入( )

| A、n≥5? | B、n>7? |
| C、n>8? | D、n≥7? |
已知变量x,y具有线性相关关系,测得(x,y)的一组数据如下:(0,1),(1,2),(2,4),(3,5),其回归方程为
=1.4x+a,则a的值等于( )
 |
| y |
| A、0.9 | B、0.8 |
| C、0.6 | D、0.2 |