题目内容
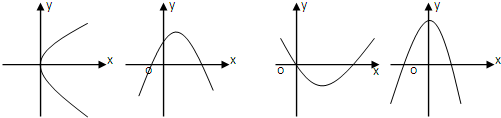
在下面的四个图象中,其中一个图象是函f(x)=
x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)的图象,则f(-1)等于( )
| 1 |
| 3 |

A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
考点:导数的运算,函数的图象
专题:函数的性质及应用
分析:求出导函数,据导函数的二次项系数为正得到图象开口向上;利用函数解析式中有2ax,故函数不是偶函数,得到函数的图象.
解答:
解:∵f′(x)=x2+2ax+(a2-1),
∴导函数f′(x)的图象开口向上.
又∵a≠0,
∴f(x)不是偶函数,其图象不关于y轴对称
其图象必为第三张图.由图象特征知f′(0)=0,
且对称轴-a>0,
∴a=-1.
则f(-1)=-
-1+1=-
,
故选:B.
∴导函数f′(x)的图象开口向上.
又∵a≠0,
∴f(x)不是偶函数,其图象不关于y轴对称
其图象必为第三张图.由图象特征知f′(0)=0,
且对称轴-a>0,
∴a=-1.
则f(-1)=-
| 1 |
| 3 |
| 1 |
| 3 |
故选:B.
点评:本题考查导函数的运算法则、二次函数的图象与二次函数系数的关系:开口方向与二次项系数的符号有关、对称轴公式.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
点P是圆C:(x-3)2+(y+4)2=4上的动点,点O为坐标原点,则|OP|的最大值为( )
| A、5 | B、6 | C、7 | D、8 |
一个几何体的三视图如图所示,则它的体积为( )


| A、40 | ||
B、
| ||
C、
| ||
D、
|
已知变量x,y具有线性相关关系,测得(x,y)的一组数据如下:(0,1),(1,2),(2,4),(3,5),其回归方程为
=1.4x+a,则a的值等于( )
 |
| y |
| A、0.9 | B、0.8 |
| C、0.6 | D、0.2 |
已知tan(α-π)=
,且α∈(
,
),则sin(α+
)=( )
| 3 |
| 4 |
| π |
| 2 |
| 3π |
| 2 |
| π |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
sin(-
)的值是( )
| 31π |
| 6 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
设偶函数f(x)的定义域为(-π,0)∪(0,π),当x∈(0,π)时,f(x)=-f′(
)sin x-πln x,若a=f(logπ3),b=f(-log39),c=f(log23),则a、b、c的大小关系为( )
| π |
| 2 |
| A、a>b>c |
| B、b>c>a |
| C、c>a>b |
| D、a>c>b |