题目内容
已知变量x，y具有线性相关关系，测得（x，y）的一组数据如下：（0，1），（1，2），（2，4），（3，5），其回归方程为
=1.4x+a，则a的值等于（ ）
 |
| y |
| A、0.9 | B、0.8 |
| C、0.6 | D、0.2 |
考点：线性回归方程
专题：概率与统计
分析：求出横标和纵标的平均数，写出样本中心点，把样本中心点代入线性回归方程，得到关于a的方程，解方程即可．
解答：
解：变量x，y具有线性相关关系，测得（x，y）的一组数据如下：（0，1），（1，2），（2，4），（3，5），
∴
=
=1.5，
=
=3，
∴这组数据的样本中心点是（1.5，3）
把样本中心点代入回归直线方程
=1.4x+a，
∴3=1.4×1.5+a，
∴a=0.9．
故选：A．
∴
. |
| x |
| 0+1+2+3 |
| 4 |
. |
| y |
| 1+2+4+5 |
| 4 |
∴这组数据的样本中心点是（1.5，3）
把样本中心点代入回归直线方程
|
| y |
∴3=1.4×1.5+a，
∴a=0.9．
故选：A．
点评：本题考查线性回归方程，解题的关键是线性回归直线一定过样本中心点，这是求解线性回归方程的步骤之一．
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
相关题目
已知点（1，3）和（3，-4）在直线l：2x-3y+a=0的两侧，则a的取值范围是（ ）
| A、（-∞，-18]∪（7，+∞） |
| B、（-18，7） |
| C、{-18，7} |
| D、不确定 |
已知tanA=
，则sin2A=（ ）
| 3 |
| 4 |
A、
| ||
B、-
| ||
C、±
| ||
D、±
|
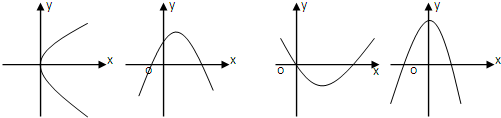
在下面的四个图象中，其中一个图象是函f（x）=
x3+ax2+（a2-1）x+1（a∈R）的导函数y=f′（x）的图象，则f（-1）等于（ ）
| 1 |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
设a∈R，函数f（x）=ex+
的导函数y=f′（x）是奇函数，若曲线y=f（x）的一条切线的斜率为
，则切点的横坐标是（ ）
| a |
| ex |
| 3 |
| 2 |
A、
| ||
B、-
| ||
| C、ln2 | ||
| D、-ln2 |
从1，2，3，4，5，6中随机抽取3个数，其和为3的倍数的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
据气象中心观察和预测：发生于M地的沙尘暴一直向正南方向移动，其移动速度v（km/h）与时间t（h）的函数图象如图所示，过线段OC上一点T（t，0）作横轴的垂线l，梯形OABC在直线l左侧部分的面积即为t（h）内沙尘暴所经过的路程s（km）．