已知函数f（x）在定义域R上的值不全为零，若函数f（x+1）的图象关于（1，0）对称，函数f（x+3）的图象关于直线x=1对称，则下列式子中错误的是（ ）
| A、f（-x）=f（x） |
| B、f（x-2）=f（x+6） |
| C、f（-2+x）+f（-2-x）=0 |
| D、f（3+x）+f（3-x）=0 |
设集合M={0，1，2}，N={x|x2-3x+2≤0}，则M∩N=（ ）
| A、{1} | B、{2} |
| C、{0，1} | D、{1，2} |
设公差不为0的等差数列{an}的前n项和为Sn，若S8=S21，ak=0，则k=（ ）
| A、14 | B、15 | C、16 | D、21 |
函数f（x）=-x3-x+sinx，当θ∈（0，
）时，恒有f（cos2θ+2msinθ）+f（-2m-2）＞0成立，则实数m的取值范围（ ）
| π |
| 2 |
A、（-∞，
| ||
B、（-∞，
| ||
C、（-
| ||
D、[-
|
设复数z=2+ai（a∈R，i是虚数单位），则
（
是z的共轭复数）是纯虚数的一个充分不必要条件是（ ）
| ||
| z |
. |
| z |
| A、a=2 | ||
| B、a=±2 | ||
C、a=
| ||
D、a=±
|
若复数z满足z•（1-i）=2-i（其中i是虚数单位），则z=（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
为了解某班学生喜爱打篮球是否与性别有关，对该班50名学生进行了问卷调查，得到如下的2×2列联表．
则至少有（ ）的把握认为喜爱打篮球与性别有关．
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
| A、95% | B、99% |
| C、99.5% | D、99.9% |
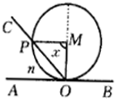如图所示，半径为2的⊙M切直线AB于O，射线OC从OA出发绕着O点顺时针旋转到OB．旋转过程中，OC交⊙M于P．记∠PMO为x，弓形PnO的面积为S=f（x），那么f（x）的图象是下图中的（ ）A、 |
B、 |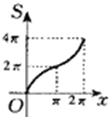
C、 |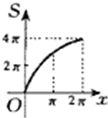
D、 |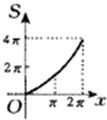
设集合M={（x，y）|y=2-x}，N={x|y=x}，则M∩N=（ ）
| A、{1，1} | B、{（1，1）} |
| C、{1} | D、∅ |
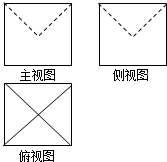某几何体的三视图如图所示，图中的四边形都是边长为1的正方形，两条虚线互相垂直，则该几何体的体积是（ ）A、
| ||
B、
| ||
C、
| ||
| D、1 |