题目内容
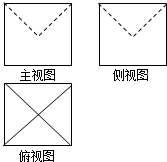 某几何体的三视图如图所示,图中的四边形都是边长为1的正方形,两条虚线互相垂直,则该几何体的体积是( )
某几何体的三视图如图所示,图中的四边形都是边长为1的正方形,两条虚线互相垂直,则该几何体的体积是( )A、
| ||
B、
| ||
C、
| ||
| D、1 |
考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:几何体是正方体挖去一个正四棱锥,判断三视图的数据所对应的几何量,并计算四棱锥的斜高与高,代入正方体与棱锥的体积公式计算.
解答:
解:由三视图知:几何体是正方体挖去一个正四棱锥,
其中正方体的边长为1,挖去的正四棱锥的斜高为
,
∴四棱锥的高为
=
,
∴几何体的体积V=13-
×12×
=
.
故选:C.
其中正方体的边长为1,挖去的正四棱锥的斜高为
| ||
| 2 |
∴四棱锥的高为
|
| 1 |
| 2 |
∴几何体的体积V=13-
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
| 6 |
故选:C.
点评:本题考查了由三视图求几何体的体积,根据三视图判断几何体的形状及数据所对应的几何量是解题的关键.

练习册系列答案
相关题目
设复数z=2+ai(a∈R,i是虚数单位),则
(
是z的共轭复数)是纯虚数的一个充分不必要条件是( )
| ||
| z |
. |
| z |
| A、a=2 | ||
| B、a=±2 | ||
C、a=
| ||
D、a=±
|
设i是虚数单位,
是复数z的共轭复数,若z=
,则
=( )
. |
| z |
| 2i3 |
| 1+i |
. |
| z |
| A、-1-i | B、1+i |
| C、-1+i | D、1-i |
设Sn是公差不为0的等差数列{an}的前n项和,S3=9,且S1,S2,S4成等比数列,则a7的值为( )
| A、7 | B、11 | C、13 | D、22 |