题目内容
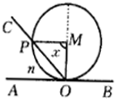 如图所示,半径为2的⊙M切直线AB于O,射线OC从OA出发绕着O点顺时针旋转到OB.旋转过程中,OC交⊙M于P.记∠PMO为x,弓形PnO的面积为S=f(x),那么f(x)的图象是下图中的( )
如图所示,半径为2的⊙M切直线AB于O,射线OC从OA出发绕着O点顺时针旋转到OB.旋转过程中,OC交⊙M于P.记∠PMO为x,弓形PnO的面积为S=f(x),那么f(x)的图象是下图中的( )A、 |
B、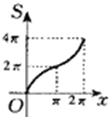 |
C、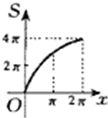 |
D、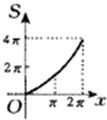 |
考点:实际问题中导数的意义,函数的图象
专题:函数的性质及应用,导数的概念及应用
分析:由题设条件,可得出弓形PnO的面积为S=f(x)的表达式,求出它的导数,研究出函数图象的变化规律,从而得出正确图象.
解答:
解:由所给的图示可得,当x≤π时,弓形PnO的面积为S=f(x)=S扇形PNO-S△MPO=2x-2sinx,其导数为f′(x)=2-2cosx,由余弦函数的性质知,此值越来越大,即f(x)的图象上升得越来越快,由此可以排除B,C;
再有所给图示的对称性知,弓形PnO的面积先是增加得越来越快,然后是增加得越来越慢,只到增加率为0,由此可以排除D
故选A.
再有所给图示的对称性知,弓形PnO的面积先是增加得越来越快,然后是增加得越来越慢,只到增加率为0,由此可以排除D
故选A.
点评:本题实际问题中导数的应用及函数图象变化规律,得出函数的表达式利用导九研究函数的单调性是解答的关键

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
在平面直角坐标平面上,
=(1,4),
=(-3,1),且
与
在直线l的方向向量上的投影的长度相等,则直线l的斜率为( )
| OA |
| OB |
| OA |
| OB |
A、-
| ||||
B、
| ||||
C、
| ||||
D、
|
设公差不为0的等差数列{an}的前n项和为Sn,若S8=S21,ak=0,则k=( )
| A、14 | B、15 | C、16 | D、21 |
复数z满足方程
=-i(i为虚数单位),则复数z在复平面内对应的点在( )
| 1+2i |
| z-3 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |