题目内容
设公差不为0的等差数列{an}的前n项和为Sn,若S8=S21,ak=0,则k=( )
| A、14 | B、15 | C、16 | D、21 |
考点:等差数列的通项公式
专题:等差数列与等比数列
分析:直接由已知结合等差数列的性质得答案.
解答:
解:在等差数列{an}中,
由S8=S21,得:a9+a10+…+a21=0,
又a9+a21=a10+a20=…=2a15,
∴13a15=0.
即a15=0.
∴k=15.
故选:B.
由S8=S21,得:a9+a10+…+a21=0,
又a9+a21=a10+a20=…=2a15,
∴13a15=0.
即a15=0.
∴k=15.
故选:B.
点评:本题考查了等差数列的通项公式,考查了等差数列的性质,是基础题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
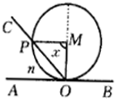 如图所示,半径为2的⊙M切直线AB于O,射线OC从OA出发绕着O点顺时针旋转到OB.旋转过程中,OC交⊙M于P.记∠PMO为x,弓形PnO的面积为S=f(x),那么f(x)的图象是下图中的( )
如图所示,半径为2的⊙M切直线AB于O,射线OC从OA出发绕着O点顺时针旋转到OB.旋转过程中,OC交⊙M于P.记∠PMO为x,弓形PnO的面积为S=f(x),那么f(x)的图象是下图中的( )A、 |
B、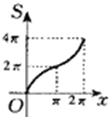 |
C、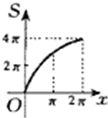 |
D、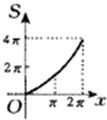 |
设i是虚数单位,
是复数z的共轭复数,若z=
,则
=( )
. |
| z |
| 2i3 |
| 1+i |
. |
| z |
| A、-1-i | B、1+i |
| C、-1+i | D、1-i |
给出下列四个结论,其中正确的是( )
| A、“a=3”是“直线l1:a2x+3y-1=0与直线l2:x-3y+2=0垂直”的充要条件 | ||||||
| B、随机变量ξ~N(0,1),若P(|ξ|≤1.96)=0.950,则P(ξ<-1.96)=0.05 | ||||||
| C、对于命题P:?x∈R使得x2+x+1<0,则¬P:?x∈R均有x2+x+1>0 | ||||||
D、在区间[0,1]上随机取一个数x,则sin
|
已知集合A={x|x>1},B={x||x|<2 },则A∩B等于( )
| A、{x|-1<x<2} |
| B、{x|x>-1} |
| C、{x|-1<x<1} |
| D、{x|1<x<2} |