在平面直角坐标系xOy中，直线l的参数方程是
x=
3
2
t+m
y=
1
2
t
（t是参数），以原点为极点，x轴的正半轴为极轴建立极坐标系，若圆C的极坐标方程是ρ=4cosθ，且直线l与圆C相切，求实数m的值．
设f（x）=x-aex（a∈R），x∈R，已知函数y=f（x）有两个零点x1，x2，且x1＜x2．
（Ⅰ）求a的取值范围；
（Ⅱ）证明：
x2
x1
随着a的减小而增大；
（Ⅲ）证明x1+x2随着a的减小而增大．
已知函数f（x）=xcosx-sinx+1（x＞0）．
（Ⅰ）求f（x）的单调区间；
（Ⅱ）记xi为f（x）的从小到大的第i（i∈N*）个零点，证明：对一切n∈N*，有
1
x
2
1
+
1
x
2
2
+…+
1
x
2
n
＜
2
3
．
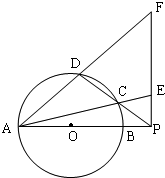如图，圆O的直径AB=10，P是AB延长线上一点，BP=2，割线PCD交圆O于点C，D，过点P做AP的垂线，交直线AC于点E，交直线AD于点F．
（1）求证：∠PEC=∠PDF；
（2）求PE•PF的值．
已知等差数列{an}的公差d大于0，且a1，a2是方程x2-14x+45=0的两根．
（1）求数列{an}的通项公式；
（2）设anan-1bn=1，求数列{bn}的前n项和Sn．
在△ABC中，a、b、c分别是角A、B、C所对的边，A=
π
3
，a=
3
，c=1，则△ABC的面积S=
 
．
设数列{an}的前n项和为Sn，且满足Sn=npan-np+n（n∈N*，p为常数），a1≠a2．
（Ⅰ）求p的值；
（Ⅱ）证明：数列{an}是等差数列．
（a+2x）（1+x）5的展开式中一次项的系数为-3，则a的值为
 
．
已知函数f（x）=
x
，x＞0
cosx，x≤0
，则f′（1）f（0）=
 
．
已知函数f（x）=ax3+|x-a|（a∈R）．
（1）是否存在实数a，使得函数f（x）在（-∞，0]上单调递减，在[0，+∞）上单调递增？请说明理由；
（2）若0＜a＜1，求函数f（x）在[-1，1]上的最大值；
（3）求证：对任意的实数a，存在x0，恒有f（x0）≠0，并求出符合该特征的x0的取值范围．
 0  211157  211165  211171  211175  211181  211183  211187  211193  211195  211201  211207  211211  211213  211217  211223  211225  211231  211235  211237  211241  211243  211247  211249  211251  211252  211253  211255  211256  211257  211259  211261  211265  211267  211271  211273  211277  211283  211285  211291  211295  211297  211301  211307  211313  211315  211321  211325  211327  211333  211337  211343  211351  266669 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网