题目内容
在平面直角坐标系xOy中,直线l的参数方程是
(t是参数),以原点为极点,x轴的正半轴为极轴建立极坐标系,若圆C的极坐标方程是ρ=4cosθ,且直线l与圆C相切,求实数m的值.
|
考点:直线的参数方程
专题:坐标系和参数方程
分析:把极坐标方程、参数方程化为直角坐标方程,根据直线和圆相切的性质求出m的值.
解答:
解:由ρ=4cosθ,得ρ2=4ρcosθ,
所以x2+y2=4x,即圆C的方程为(x-2)2+y2=4.
又由
消t,得x-
y-m=0,由直线l与圆C相切,
所以
=2,
即m=-2或m=6.
所以x2+y2=4x,即圆C的方程为(x-2)2+y2=4.
又由
|
| 3 |
所以
| |2-m| |
| 2 |
即m=-2或m=6.
点评:本题主要考查把极坐标方程、参数方程化为直角坐标方程的方法,点到直线的距离公式的应用,直线和圆的位置关系,属于基础题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
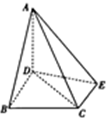 在三棱椎A-BCD中,AB=BC=4,AD=BD=CD=2
在三棱椎A-BCD中,AB=BC=4,AD=BD=CD=2