题目内容
已知函数f(x)=
,则f′(1)f(0)= .
|
考点:导数的运算,分段函数的应用
专题:函数的性质及应用
分析:根据分段函数的表达式,求函数的导数,进行求解即可.
解答:
解:由分段函数可知,f(0)=cos0=1,
当x>0时,f(x)=
,则f′(x)=
,
得f′(1)=
,
则f′(1)f(0)=
×1=
,
故答案为:
.
当x>0时,f(x)=
| x |
| 1 | ||
2
|
得f′(1)=
| 1 |
| 2 |
则f′(1)f(0)=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题主要考查函数值的计算,利用分段函数的表达式分别求解是解决本题的关键,比较基础.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 如图,正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB∥CD.AB=AD=
如图,正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB∥CD.AB=AD=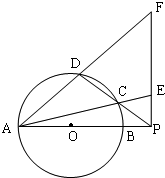 如图,圆O的直径AB=10,P是AB延长线上一点,BP=2,割线PCD交圆O于点C,D,过点P做AP的垂线,交直线AC于点E,交直线AD于点F.
如图,圆O的直径AB=10,P是AB延长线上一点,BP=2,割线PCD交圆O于点C,D,过点P做AP的垂线,交直线AC于点E,交直线AD于点F.