题目内容
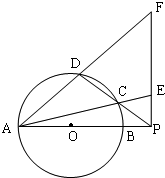如图，圆O的直径AB=10，P是AB延长线上一点，BP=2，割线PCD交圆O于点C，D，过点P做AP的垂线，交直线AC于点E，交直线AD于点F．（1）求证：∠PEC=∠PDF；
（2）求PE•PF的值．
考点：与圆有关的比例线段
专题：选作题,立体几何
分析：（1）证明P、B、C、E四点共圆、A、B、C、D四点共圆，利用四点共圆的性质，即可证明：∠PEC=∠PDF；
（2）证明D，C，E，F四点共圆，利用割线定理，即可求得PE•PF的值．
（2）证明D，C，E，F四点共圆，利用割线定理，即可求得PE•PF的值．
解答：
（1）证明：连结BC，∵AB是圆O的直径，∴∠ACB=∠APE=90°，
∴P、B、C、E四点共圆．
∴∠PEC=∠CBA．
又∵A、B、C、D四点共圆，∴∠CBA=∠PDF，
∴∠PEC=∠PDF----（5分）
（2）解：∵∠PEC=∠PDF，∴F、E、C、D四点共圆．
∴PE•PF=PC•PD=PA•PB=2×12=24．----（10分）
（1）证明：连结BC，∵AB是圆O的直径，∴∠ACB=∠APE=90°，∴P、B、C、E四点共圆．
∴∠PEC=∠CBA．
又∵A、B、C、D四点共圆，∴∠CBA=∠PDF，
∴∠PEC=∠PDF----（5分）
（2）解：∵∠PEC=∠PDF，∴F、E、C、D四点共圆．
∴PE•PF=PC•PD=PA•PB=2×12=24．----（10分）
点评：本题考查圆的性质，考查四点共圆的判定，考查割线的性质，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
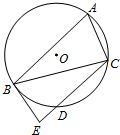如图，A，B，C是⊙O上的三点，BE切⊙O于点B，D是CE与⊙O的交点．若∠BAC=60°，BC=2BE，求证：CD=2ED．
已知函数f（x）=lnx，g（x）=