题目内容

（a+2x）（1+x）5的展开式中一次项的系数为-3，则a的值为
 
．
考点：二项式系数的性质
专题：二项式定理
分析：（a+2x）（1+x）5的展开式中x项由两部分相加得到：①（a+2x）中的常数项与（1+x）6展开式中的x5项 ②（1+x）中的x项与（1+x）6展开式中的x4项．分别求的系数再相加即可．
解答： 解：∵（a+2x）（1+x）5的展开式中x项由两部分相加得到：
①（a+2x）中的常数项与（1+x）5展开式中的x项
②（a+2x）中的x项与（1+x）5展开式中的常数项．分别求的系数乘积再相加即可．
（1+x）5展开式中的常数项为1，（1+x）5展开式中的x项的系数为：5．
∵（a+2x）（1+x）5的展开式中一次项的系数为-3，
∴-3=5a+2．
∴a=-1；
故答案为：-1．
点评：本题考查二项式定理的应用，要注意本题中所求系数应由两部分组成．否则易出错．
练习册系列答案
相关题目
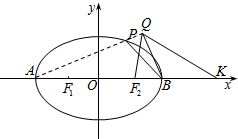椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）上的任意一点P（x0，y0）（左、右顶点A，B除外）与两焦点F1（-2，0），F2（2，0）围成的三角形的周长恒为12．
（1）求椭圆C的方程；
（2）若动点Q（x，y）到点F2与到K（8，0）距离之比为
1
2
，求点Q的轨迹E的方程；
（3）设直线PB，QB的斜率分别为k1，k2，且4k1=3k2，证明：A，P，Q三点共线．
某次数学考试中有三道选做题，分别为选做题1、2、3．规定每位考生必须且只须在其中选做一题．甲、乙、丙三名考生选做这一题中任意一题的可能性均为
1
3
，每位学生对每题的选择是相互独立的，各学生的选择相互之间没有影响．
（1）求这三个人选做的是同一道题的概率：
（2）设ξ为三个人中做选做题l的人数，求ξ的分布列与均值．
曲线C极坐标方程为ρ2-4ρcosθ-4ρsinθ+6=0，以极点为原点，极轴为x轴正半轴建立直角坐标系，直线l的参数方程为
x=-2-
2
t
y=3+
2
t
（t为参数），则曲线C上的点到直线l的距离的最小值为
 
．
已知
a
=（sinα，1），
b
=（cosα，2），α∈（0，
π
4
）．
（1）若
a
•
b
=
17
8
，求sinα-cosα的值；
（2）若
a
∥
b
，又β为锐角，且tanβ=
1
3
，求α+β的值．
已知函数f（x）=xcosx-sinx+1（x＞0）．
（Ⅰ）求f（x）的单调区间；
（Ⅱ）记xi为f（x）的从小到大的第i（i∈N*）个零点，证明：对一切n∈N*，有
1
x
2
1
+
1
x
2
2
+…+
1
x
2
n
＜
2
3
．
已知函数y=f（x）是定义在R上的奇函数，对?x∈R都有f（x-1）=f（x+1）成立，当x∈（0，1]且x1≠x2时，有
f(x2)-f(x1)
x2-x1
＜0．给出下列命题：
（1）f（1）=0
（2）f（x）在[-2，2]上有3个零点   
（3）（2014，0）是函数y=f（x）的一个对称中心  
（4）直线x=1是函数y=f（x）图象的一条对称轴．
其中正确命题的编号为
 
．
观察下列问题：
已知（1-2x）2014=a0+a1x+a2x2+a3x3+…+a2014x2014，令x=1，可得a0+a1+a2+…+a2014=（1-2×1）2014=1，令x=-1，可得a0-a1+a2-a3+…+a2014=（1+2×1）2014=32014请仿照这种“赋值法”，令x=0，得到a0=
 
，并求出
a1
2
+
a2
22
+
a3
23
+…+
a2014
22014
=
 
．
已知点A（0，-3），B（4，0），点P是圆x2+y2-2y=0上任意一点，则△ABP面积的最小值是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网