设全集U=R，集合A={x|0≤x≤2}，B={y|1≤y≤3}，则（∁UA）∩B=（ ）
| A、（2，3] |
| B、（-∞，1]∪（2，+∞） |
| C、[1，2） |
| D、（-∞，0）∪[1，+∞） |
已知三棱锥的三视图如图所示，则它的体积为（ ）
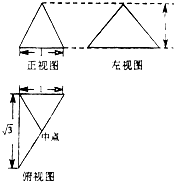
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知i为虚数单位，a为实数，复数z=（a-2i）•i在复平面内对应的点为M，则“a=-1”是“点M在第四象限”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
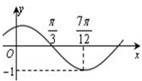f（x）=Acos（ωx+φ）（A，ω＞0）的图象如图所示，为得到g（x）=-Asin（ωx+| π |
| 6 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
已知i为虚数单位，复数z=-
+
i的共轭复数为
，则
+|z|（ ）
| 1 |
| 2 |
| ||
| 2 |
. |
| z |
. |
| z |
A、-
| ||||||
B、
| ||||||
C、
| ||||||
D、-
|
己知命题“?x∈R，使x2+（a+1）x+1≤0”是假命题，则实数a的取值范围是（ ）
| A、（-∞，-3）∪（1，+∞） |
| B、（-∞，-3]∪[1，+∞） |
| C、（-3，1） |
| D、[-3，1] |
设等差数列{an}的前n项和为Sn，若a1=1，a2+a3=11，则S6-S3=（ ）
| A、27 | B、39 | C、45 | D、63 |
下列四个图中，函数y=
的图象可能是（ ）
| 10ln|x+1| |
| x+1 |
A、 |
B、 |
C、 |
D、 |
从6名教师中选4名开设A，B，C，D四门课程，每人开设一门课程且开设的课程各不相同，若这6名教师中甲、乙两人不开设A课程，则不同的选择方案共有（ ）
| A、300种 | B、240种 |
| C、144种 | D、96种 |
已知tan2α=
，α∈（0，
），则
=（ ）
| 3 |
| 4 |
| π |
| 4 |
| sinα+cosα |
| sinα-cosα |
| A、1 | B、-1 | C、2 | D、-2 |