题目内容
从6名教师中选4名开设A，B，C，D四门课程，每人开设一门课程且开设的课程各不相同，若这6名教师中甲、乙两人不开设A课程，则不同的选择方案共有（ ）
| A、300种 | B、240种 |
| C、144种 | D、96种 |
考点：排列、组合及简单计数问题
专题：应用题,排列组合
分析：根据题意，按甲乙是否参加分3种情况讨论：①选出的4人不含甲乙，②选出的4人只含甲、乙中的一人，③选出的4人含甲、乙二人，甲乙均参加，由排列、组合公式分别求出每种情况下的选择方案数目，由分类计数原理将其相加即可得答案．
解答：
解：根据题意，需要从6名教师中选4名，按甲乙是否参加分3种情况讨论：
①选出的4人不含甲乙，将剩余的4人全排列，对应四门课程即可，有A44=24种选择方案，
②选出的4人只含甲、乙中的一人，
甲或乙参加有2种情况，在剩余4人中选出三人，有C43=4种选法，
此时甲有3门课程可选，剩余3人全排列，对应其他三门课程即可，共有3A33=18种方案，
此时有2×4×18=144种选择方案，
③选出的4人含甲、乙二人，甲乙均参加，有1种情况，
在剩余4人中选出2人，有C42=6种选法，
此时甲、乙有A32=6种情况，剩余2人全排列，对应其他二门课程即可，共有6A22=12种方案，
此时有1×6×12=72种选择方案，
共有24+144+72=240种选择方案；
故选：B．
①选出的4人不含甲乙，将剩余的4人全排列，对应四门课程即可，有A44=24种选择方案，
②选出的4人只含甲、乙中的一人，
甲或乙参加有2种情况，在剩余4人中选出三人，有C43=4种选法，
此时甲有3门课程可选，剩余3人全排列，对应其他三门课程即可，共有3A33=18种方案，
此时有2×4×18=144种选择方案，
③选出的4人含甲、乙二人，甲乙均参加，有1种情况，
在剩余4人中选出2人，有C42=6种选法，
此时甲、乙有A32=6种情况，剩余2人全排列，对应其他二门课程即可，共有6A22=12种方案，
此时有1×6×12=72种选择方案，
共有24+144+72=240种选择方案；
故选：B．
点评：本题考查排列、组合的应用，涉及分类加法原理，分类讨论的关键在于确定分类讨论的依据、标准，一定做到不重不漏．
练习册系列答案
相关题目
复数z1=2+i，z2=
在复平面上分别对应点A，B，则∠AOB=（ ）
| 1 |
| 3+i |
A、
| ||
B、
| ||
C、
| ||
D、
|
若直线xcosθ+ysinθ+1=0与圆（x+1）2+（y-1）2=1相切，且θ为锐角，则该直线的斜率是（ ）
| A、1 | ||
B、-
| ||
| C、-1 | ||
D、
|
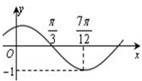f（x）=Acos（ωx+φ）（A，ω＞0）的图象如图所示，为得到g（x）=-Asin（ωx+| π |
| 6 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
已知f（x）是定义在（0，+∞）的单调函数，且对任意的x∈（0，+∞），都有f[f（x）-lnx]=1，则函数g（x）=ex-f（x）+1的最小值必在区间（ ）
A、（
| ||
B、（2，
| ||
| C、（1，2） | ||
D、（
|