题目内容
已知i为虚数单位,复数z=-
+
i的共轭复数为
,则
+|z|( )
| 1 |
| 2 |
| ||
| 2 |
. |
| z |
. |
| z |
A、-
| ||||||
B、
| ||||||
C、
| ||||||
D、-
|
考点:复数的基本概念,复数求模
专题:数系的扩充和复数
分析:根据复数的有关概念,即可得到结论.
解答:
解:∵z=-
+
i的共轭复数为
,
∴
=-
-
i,|z|=
=1,
则
+|z|=-
-
i+1=z=
-
i,
故选:B
| 1 |
| 2 |
| ||
| 2 |
. |
| z |
∴
. |
| z |
| 1 |
| 2 |
| ||
| 2 |
(-
|
则
. |
| z |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
故选:B
点评:本题主要考查复数的基本运算,比较基础.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
已知全集U=R,集合A={x|y=log2(-x2+2x)},B={y|y≥1},则A∩∁UB=( )
| A、{x|0<x<1} |
| B、{x|x<0} |
| C、{x|x>2} |
| D、{x|1<x<2} |
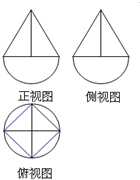 某几何体的三视图如图所示,其中正视图由直径为2的半圆和等边三角形构成,则该几何体的体积为( )
某几何体的三视图如图所示,其中正视图由直径为2的半圆和等边三角形构成,则该几何体的体积为( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
复数
在复平面内所对应的点在实轴上,那么实数a=( )
| a+i |
| 2-i |
| A、-2 | B、0 | C、1 | D、2 |
已知tan2α=
,α∈(0,
),则
=( )
| 3 |
| 4 |
| π |
| 4 |
| sinα+cosα |
| sinα-cosα |
| A、1 | B、-1 | C、2 | D、-2 |
若函数f(x)为偶函数,x>0时,f(x)递增,P=f(-π),Q=f(e),R=f(lnπ),则( )
| A、P>Q>R |
| B、R>Q>P |
| C、P>R>Q |
| D、Q>R>P |
现有1位教师,2位男同学,3位女同学共6人站成一排,要求2位男同学站两边,3位女同学中有且仅有两位相邻,则不同排法有( )
| A、12种 | B、24种 |
| C、36种 | D、72种 |
| 2sin40°-cos10° |
| sin10° |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
 已知椭圆C:
已知椭圆C: