题目内容
设等差数列{an}的前n项和为Sn,若a1=1,a2+a3=11,则S6-S3=( )
| A、27 | B、39 | C、45 | D、63 |
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:由已知条件利用等差数列的通项公式求出公差d,由此利用等差数列的前n项和公式能求出结果.
解答:
解:∵等差数列{an}的前n项和为Sn,
a1=1,a2+a3=11,
∴1+d+1+2d=11,解得d=3,
∴S6-S3=(6+
d)-(3+
d)
=3+12d
=39.
故选:B.
a1=1,a2+a3=11,
∴1+d+1+2d=11,解得d=3,
∴S6-S3=(6+
| 6×5 |
| 2 |
| 3×2 |
| 2 |
=3+12d
=39.
故选:B.
点评:本题考查等差数列的前n项和的差的求法,是基础题,解题时要注意等差数列的通项公式的合理运用.

练习册系列答案
相关题目
等差数列{an}的前n项的和为Sn,且S7-S4=4π,则tana6=( )
| A、1 | ||||
B、
| ||||
C、
| ||||
| D、2 |
若0<
<
的解集记为p,关于x的不等式x2+(a-1)x-a>0的解集记为q,且p是q的充分不必要条件,则实数a的取值范围是( )
| 1 |
| x |
| 1 |
| 2 |
| A、(-2,-1] |
| B、[-2,-1] |
| C、[-1,+∞) |
| D、[-2,+∞) |
设变量x,y满足
,若目标函数z=x-y+1的最小值为0,则m的值为( )
|
| A、4 | B、5 | C、6 | D、7 |
已知三棱锥的三视图如图所示,则它的体积为( )
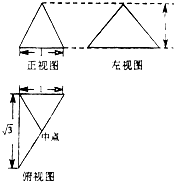

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知向量
=(1,2),
=(2,-1),下列结论中不正确的是( )
| a |
| b |
A、|
| ||||||||
B、
| ||||||||
C、|
| ||||||||
D、
|
设曲线C的参数方程为
(t为参数),若以直角坐标系的原点为极点,x轴的正半轴为极轴建立极坐标系,则曲线C的极坐标方程为( )
|
| A、sinθ=ρcos2θ |
| B、sinθ=ρcosθ |
| C、2sinθ=ρcos2θ |
| D、sinθ=2ρcos2θ |