题目内容
已知i为虚数单位，a为实数，复数z=（a-2i）•i在复平面内对应的点为M，则“a=-1”是“点M在第四象限”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：数系的扩充和复数
分析：根据充分条件和必要条件的定义，利用复数的几何意义，即可得到结论．
解答：
解：z=（a-2i）•i=2+ai，对应的坐标为M（2，a），
若a=-1，则M（2，-1）在第四象限，即充分性成立．
若M（2，a）在第四象限，则a＜0，即必要性不成立，
故“a=-1”是“点M在第四象限”的充分不必要条件，
故选：A．
若a=-1，则M（2，-1）在第四象限，即充分性成立．
若M（2，a）在第四象限，则a＜0，即必要性不成立，
故“a=-1”是“点M在第四象限”的充分不必要条件，
故选：A．
点评：本题主要考查充分条件和必要条件的应用，利用复数的几何意义是解决本题的关键．比较基础．
练习册系列答案
相关题目
复数
（i为虚数单位）的模等于（ ）
| 1+i |
| i |
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|
已知sin2α=
，则cos2（α-
）=（ ）
| 1 |
| 3 |
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
| a |
| b |
| a |
| b |
| a |
| b |
| A、锐角 | B、直角 | C、钝角 | D、π |
下列四个图中，函数y=
的图象可能是（ ）
| 10ln|x+1| |
| x+1 |
A、 |
B、 |
C、 |
D、 |
已知向量
与向量
的夹角为90°，且|
|=1，|
|=2，若
=
+λ
，
⊥（2
-
），则实数λ的值为（ ）
| a |
| b |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
A、λ=
| ||
B、λ=
| ||
C、λ=
| ||
| D、λ=1 |
某校对高三年级1200名学生进行健康检查，按性别用分层抽样的方法抽取一个容量为120人的样本．已知女生抽到了55人，则该校男生的人数是（ ）
| A、65 | B、550 |
| C、600 | D、650 |
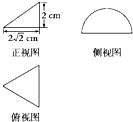一个几何体的三视图及其尺寸如图所示，其中正视图是直角三角形，侧视图是半圆，俯视图是等腰三角形，则这个几何体的表面积为（ ）A、2（1+2
| ||||
B、2（1+
| ||||
C、4（1+
| ||||
D、2（2+
|