题目内容
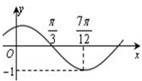f（x）=Acos（ωx+φ）（A，ω＞0）的图象如图所示，为得到g（x）=-Asin（ωx+| π |
| 6 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：由函数的最值求出A，由周期求出ω，由五点法作图求出φ的值，可得函数f（x）的解析式．再根据函数y=Asin（ωx+φ）的图象变换规律，得出结论．
解答：
解：由题意可得A=1，
T=
•
=
-
，解得ω=2，
∴f（x）=Acos（ωx+φ）=2cos（2x+φ）．
再由五点法作图可得 2×
+φ=
，∴φ=-
，
∴f（x）=2cos（2x-
）=2cos2（x-
），
g（x）=-2sin（2x+
）=2cos（2x+
+
）=2cos2（x+
），
而
-（-
）=
，
故将f（x）的图象向左平移
个单位长度，即可得到函数g（x）的图象，
故选：D．
| 1 |
| 4 |
| 1 |
| 4 |
| 2π |
| ω |
| 7π |
| 12 |
| π |
| 3 |
∴f（x）=Acos（ωx+φ）=2cos（2x+φ）．
再由五点法作图可得 2×
| π |
| 3 |
| π |
| 2 |
| π |
| 6 |
∴f（x）=2cos（2x-
| π |
| 6 |
| π |
| 12 |
g（x）=-2sin（2x+
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
而
| π |
| 3 |
| π |
| 12 |
| 5π |
| 12 |
故将f（x）的图象向左平移
| 5π |
| 12 |
故选：D．
点评：本题主要考查由函数y=Asin（ωx+φ）的部分图象求解析式，函数y=Asin（ωx+φ）的图象变换规律，属于中档题．
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
已知两个实数a，b（a≠b），满足aea=beb，命题p：lna+a=lnb+b；命题q：（a+1）（b+1）＜0．则下面命题正确的是（ ）
| A、p真q假 | B、p假q真 |
| C、p真q真 | D、p假q假 |
已知集合M={x|x2+2x-3＞0}，N={x|y=
}，则（∁RM）∪N为（ ）
| ||
| ln(2x-x2) |
| A、[-3，2） |
| B、（-2，3] |
| C、[-3，1）∪（1，2） |
| D、[-1，2） |
公差不为零的等差数列{an}的前n项和为Sn，若a3是a2与a6的等比中项，S4=8，则S6=（ ）
| A、18 | B、24 | C、60 | D、90 |
从6名教师中选4名开设A，B，C，D四门课程，每人开设一门课程且开设的课程各不相同，若这6名教师中甲、乙两人不开设A课程，则不同的选择方案共有（ ）
| A、300种 | B、240种 |
| C、144种 | D、96种 |
某几何体的三视图如图所示，则它的体积是（ ）
| A、5 | ||
| B、6 | ||
C、
| ||
D、
|
（
+
）10的展开式中常数项为（ ）
| x |
| 1 | |||
|
| A、120 | B、210 |
| C、252 | D、45 |
已知等差数列{an}中，a3+a4=a12，a1+a2=10，则a2+a4+…a100的值等于（ ）
| A、1300 | ||
| B、1350 | ||
| C、2650 | ||
D、
|